Question

【题目】对于平面内任意一个角的“夹线圆”，给出如下定义：如果一个圆与这个角的两边都相切，则称这个圆为这个角的“夹线圆”.例如：在平面直角坐标系xOy中，以点（1，1）为圆心，1为半径的圆是x轴与y轴所构成的直角的“夹线圆”.

(1)下列各点中，可以作为x轴与y轴所构成的直角的“夹线圆”的圆心的点是哪些；

A（2，2），B（3，1），C（-1，0），D（1，-1）

(2)若⊙P为y轴和直线 l：所构成的锐角的“夹线圆”，且⊙P的半径为1，求点P的坐标.

(3)若 ⊙Q为x轴和直线所构成的锐角的“夹线圆”，且⊙Q的半径，直接写出点Q横坐标的取值范围.

Answer 1

【答案】（1）A，D； （2）P点坐标为，（3）

【解析】

（1）由点A的横纵坐标相等及点D的横纵坐标的绝对值相等，可得出点A，D能作为x轴与y轴所构成的直角的“夹线圆”的圆心；
（2）过P点作PE⊥y轴于点E，PF⊥直线l于点F，连PO，设直线l与x轴夹角为α，由直线l的解析式可得出α=30°及∠EOF=60°，由⊙P与y轴及直线OF均相切可得出∠EOP=30°，结合EP=1可求出OE=，进而可得出点E的坐标；
（3）过Q点作QM⊥x轴于点M，QN⊥直线y=-x+2于点N，延长MQ交直线y=-x+2于点G，设直线y=-x+2与x轴交于点S，利用一次函数图象上点的坐标特征可得出点S的坐标，由∠MSG=30°，∠MGS=60°可得出MS=MGtan60°=（2+）r，结合1≤r≤2可得出MS的取值范围，再将其代入xQ=6+MS或xQ=6-MS即可得出点Q横坐标xQ的取值范围．

（1））∵2=2，1=|-1|，
∴点A，D能作为x轴与y轴所构成的直角的“夹线圆”的圆心．

故答案为：点A， D能作为x轴与y轴所构成的直角的“夹线圆”的圆心．

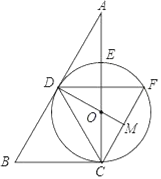
（2）如图：过P点作PA⊥y轴于点A，PB⊥l于B，连PO.

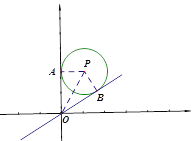
∵点B为直线上一点

∴设B点坐标为（x，）

设直线与x轴夹角为

∴直线 l与x轴的夹角为30°

∴∠AOB=60°

又∵⊙P与x轴及直线OB均相切，

∴OP平分∠AOB

∴∠AOP=30°

又∵AP=1

∴P点坐标为

同理，当P点在第三象限时，P点坐标为

（3）

理由：如图2，过Q点作QM⊥x轴于点M，QN⊥直线y=-x+2

于点N，延长MQ交直线y=-x+2于点G，设直线y=-x+2与x轴交于点S．

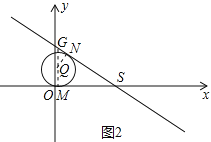
当y=0时，有-x+2=0，
解得：x=6，
∴点S的坐标为（6，0）．
∵∠MSG=30°，
∴∠MGS=60°，
∴MG=MQ+QG=r+ =r ，
∴MS=MGtan60°=（2+）r，
∵⊙Q的半径1≤r≤2，
∴2+≤MS≤4+2，
∴2-2≤6-MS≤4-，8+≤6+MS≤10+2，
∴点Q横坐标xQ的取值范围为：2-2≤xQ≤4-或8+≤xQ≤10+2．