Ő‚ńŅńŕ»›
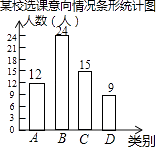
°ĺŐ‚ńŅ°Ņő™…ÓĽĮ“ŚőŮĹŐ”żŅő≥ŐłńłÔ£¨¬ķ◊„—ß…ķĶńłŲ–‘ĽĮ—ßŌį–Ť«ů£¨ń≥–£ĺÕ°į—ß…ķ∂‘÷™ ∂Õō’Ļ£¨ŐŚ”żŐō≥§°Ę“’ űŐō≥§ļÕ ĶľýĽÓ∂Įňńņŗ—°Ņő“‚ŌÚ°ĪĹÝ––Ńň≥ť—ýĶų≤ť£®√Ņ»ň—°Ī®“Ľņŗ£©£¨Ľś÷∆Ńň»ÁÕľňý ĺĶńŃĹ∑ýÕ≥ľ∆Õľ£®≤ĽÕÍ’Ż£©£¨«Žłýĺ›Õľ÷––ŇŌĘ£¨Ĺ‚īūŌ¬Ń–ő Ő‚£ļ
£®1£©«ů…»–őÕ≥ľ∆Õľ÷–mĶń÷Ķ£¨≤Ę≤Ļ»ęŐű–őÕ≥ľ∆Õľ£Ľ
£®2£©‘ŕĪĽĶų≤ťĶń—ß…ķ÷–£¨ňśĽķ≥ť“Ľ»ň£¨≥ťĶĹ—°°įŐŚ”żŐō≥§ņŗ°ĪĽÚ°į“’ űŐō≥§ņŗ°ĪĶń—ß…ķĶńłŇ¬ «∂ŗ…Ŕ£Ņ
£®3£©“—÷™ł√–£”–800√Ż—ß…ķ£¨ľ∆ĽģŅ™…Ť°į ĶľýĽÓ∂Įņŗ°ĪŅő≥Ő√Ņįŗį≤ŇŇ20»ň£¨ő —ß–£Ņ™…Ť∂ŗ…ŔłŲ°į ĶľýĽÓ∂Įņŗ°ĪŅő≥ŐĶńįŗľ∂Ī»ĹŌļŌņŪ£Ņ
°ĺīūįł°Ņ
£®1£©Ĺ‚£ļ◊‹»ň ż=15°¬25%=60£®»ň£©£ģ
Aņŗ»ň ż=60©Ā24©Ā15©Ā9=12£®»ň£©£ģ
°Ŗ12°¬60=0.2=20%£¨
°ŗm=20£ģ
Őű–őÕ≥ľ∆Õľ»ÁÕľ£Ľ
£®2£©Ĺ‚£ļ≥ťĶĹ—°°įŐŚ”żŐō≥§ņŗ°ĪĽÚ°į“’ űŐō≥§ņŗ°ĪĶń—ß…ķĶńłŇ¬ = ![]() =
= ![]()
£®3£©Ĺ‚£ļ°Ŗ800°Ń25%=200£¨200°¬20=10£¨
°ŗŅ™…Ť10łŲ°į Ķ—ťĽÓ∂Įņŗ°ĪŅő≥ŐĶńįŗľ∂ żĪ»ĹŌļŌņŪ
°ĺĹ‚őŲ°Ņ£®1£©ŃĹłŲÕľ“™ĹŠļŌ∆ūņī£¨Őű–őÕ≥ľ∆ÕľĶń≤Ļ»ęĻōľŁ ««ů≥Ųňý»Ī≤Ņ∑÷Ķń żŃŅ£¨≤Ņ∑÷ ![]() įŔ∑÷Ī»=◊‹ ż£¨ĺŖŐŚŃŅ=—ýĪĺ»›ŃŅ
įŔ∑÷Ī»=◊‹ ż£¨ĺŖŐŚŃŅ=—ýĪĺ»›ŃŅ![]() Ōŗ”¶įŔ∑÷Ī»£Ľ£®2£©ņŻ”√łŇ¬ Ļę ĹľīŅ…;£®3£©ņŻ”√°į—ýĪĺĶńįŔ∑÷Ī»Ņ…“‘Ļņľ∆◊‹ŐŚĶńįŔ∑÷Ī»°Ī£¨Ķ√≥ŲĹŠĻŻ.
Ōŗ”¶įŔ∑÷Ī»£Ľ£®2£©ņŻ”√łŇ¬ Ļę ĹľīŅ…;£®3£©ņŻ”√°į—ýĪĺĶńįŔ∑÷Ī»Ņ…“‘Ļņľ∆◊‹ŐŚĶńįŔ∑÷Ī»°Ī£¨Ķ√≥ŲĹŠĻŻ.
°ĺŅľĶ„ĺęőŲ°ŅĻō”ŕĪĺŐ‚Ņľ≤ťĶń…»–őÕ≥ľ∆ÕľļÕŐű–őÕ≥ľ∆Õľ£¨–Ť“™ŃňĹ‚ń‹«Ś≥ĢĶōĪŪ ĺ≥Ųłų≤Ņ∑÷‘ŕ◊‹ŐŚ÷–ňý’ľĶńįŔ∑÷Ī»£ģĶę «≤Ľń‹«Ś≥ĢĶōĪŪ ĺ≥Ų√ŅłŲŌÓńŅĶńĺŖŐŚ żńŅ“‘ľį ¬őÔĶńĪšĽĮ«ťŅŲ£Ľń‹«Ś≥ĢĶōĪŪ ĺ≥Ų√ŅłŲŌÓńŅĶńĺŖŐŚ żńŅ£¨Ķę «≤Ľń‹«Ś≥ĢĶōĪŪ ĺ≥ŲłųłŲ≤Ņ∑÷‘ŕ◊‹ŐŚ÷–ňý’ľĶńįŔ∑÷Ī»“‘ľį ¬őÔĶńĪšĽĮ«ťŅŲ≤Ňń‹Ķ√≥Ų’ż»∑īūįł£ģ

 –¬ŅőĪÍĹ◊Ő›‘ń∂Ń—ĶŃ∑ŌĶŃ–īūįł
–¬ŅőĪÍĹ◊Ő›‘ń∂Ń—ĶŃ∑ŌĶŃ–īūįł Ņŕň„–ńň„ňŔň„”¶”√Ő‚ŌĶŃ–īūįł
Ņŕň„–ńň„ňŔň„”¶”√Ő‚ŌĶŃ–īūįł Õ¨≤ĹÕō’Ļ‘ń∂ŃŌĶŃ–īūįł
Õ¨≤ĹÕō’Ļ‘ń∂ŃŌĶŃ–īūįł





