Question

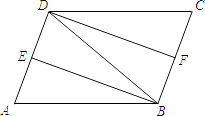
【题目】如图所示，ABCD中，E，F分别是AB、CD上的点，AE＝CF，M、N分别是DE、BF的中点．

（1）求证：四边形ENFM是平行四边形．

（2）若∠ABC＝2∠A，求∠A的度数．

Answer 1

【答案】（1）见解析；（2）∠A＝60°

【解析】

（1）先证△ADE≌△CBF（SAS），得DE=BF，∠AED＝∠CFB，进而得ME＝FN，∠AED＝∠ABF，即ME∥FN，由此得证；

（2）由平行线的性质得∠A+∠ABC＝180°，据此计算得解．

（1）证明：∵四边形ABCD是平行四边形，

∴AD＝BC，∠A＝∠C．

又∵AE＝CF，

∴△ADE≌△CBF（SAS），

∴∠AED＝∠CFB，DE＝BF，

由四边形ABCD是平行四边形，

∴DC∥AB．

∴∠CFB＝∠ABF．

∴∠AED＝∠ABF．

∴ME∥FN，

又∵M、N分别是DE、BF的中点，且DE＝BF，

∴ME＝FN．

∴四边形ENFM是平行四边形；

（2）∵四边形ABCD是平行四边形，

∴∠A+∠ABC＝180°，

又∵∠ABC＝2∠A，

∴3∠A＝180°，

∴∠A＝60°．