题目内容
【题目】我们给抛物线y＝a（x﹣h）2＋k（a≠0）定义一种变换，先作这条抛物线关于原点对称的抛物线
，再将得到的对称抛物线向上平移m（m＞0）个单位长度，得到新的抛物线ym，则我们称ym为二次函数y＝a（x﹣h）2＋k（a≠0）的m阶变换．若抛物线M的6阶变换的关系式为
．
（1）抛物线M的函数表达式为 ；
（2）若抛物线M的顶点为点A，与r轴相交的两个交点中的左侧交点为点B，则在抛物线上是否存在点P，使点P与直线AB的距离最短？若存在，请求出此时点P的坐标．
【答案】（1）y＝﹣（x＋1）2＋1 ；（2）存在， P(
，
)
【解析】
（1）6阶变换的关系式对应的函数顶点为：(1，5)，则函数M的顶点为：(﹣1，1)，即可求解；
（2）根据待定系数法求出直线AB的解析式，再由DP＝
PH＝（x2﹣2x＋6﹣x﹣2）＝（x2﹣3x＋4），根据二次函数的性质即可求解．
（1）6阶变换的关系式对应的函数顶点为：(1，5)，将顶点坐标先向下平移6个单位长度，再关于原点对称，
∴变换前函数M的顶点为：(﹣1，1)，
∴函数M的表达式为：y＝﹣（x＋1）2＋1，
故答案为：y＝﹣（x＋1）2＋1；
（2）存在，理由：
y＝﹣（x＋1）2＋1，令y＝0，则x＝﹣2或0，
故点B(﹣2，0)，而点A(﹣1，1)，
将点A、B的坐标代入一次函数表达式：y＝kx＋b得：
，解得：
，
故直线AB的函数表达式为：y＝x＋2，
y6′＝（x﹣1）2＋5＝x2﹣2x＋6，
如下图，过点P作PD⊥AB交于点D，故点P作y轴的平行线交AB于点H，
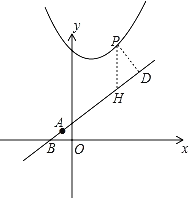
∵直线AB的倾斜角为45°，则DP＝PH，
设点P（x，x2﹣2x＋6），则点H（x，x＋2），
DP＝PH＝（x2﹣2x＋6﹣x﹣2）＝（x2﹣3x＋4），
∵＞0，故DP有最小值，此时x＝，
故点P(，)．
