题目内容
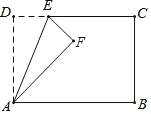
【题目】在四边形ABCD中,AB∥CD,∠A=90![]() ,AB=
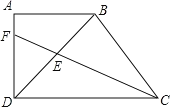
,AB=![]() ,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△CDE的面积为_____.
,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△CDE的面积为_____.
【答案】![]() .
.
【解析】
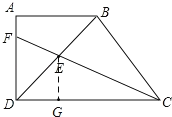
先过点E作EG⊥CD于G,再判定△BCD.△ABD都是等腰直角三角形,并求得其边长,最后利用角平分线的性质和等腰直角三角形的性质,求得EG的长,进而得到△EDC的面积.
过点E作EG⊥CD于G.
又∵CF平分∠BCD,BD⊥BC,∴BE=GE,BC=GC.
∵BD⊥BC,BD=BC,∴△BCD是等腰直角三角形,∴∠BDC=45°.
∵AB∥CD,∴∠ABD=45°.
又∵∠A=90°,AB=![]() ,∴等腰直角三角形ABD中,BD
,∴等腰直角三角形ABD中,BD![]() ,∴BC=2,∴Rt△BDC中,CD
,∴BC=2,∴Rt△BDC中,CD![]() ,∴DG=DC﹣GC=
,∴DG=DC﹣GC=![]() .
.
∵△DEG是等腰直角三角形,∴EG=DG=![]() ,∴△EDC的面积
,∴△EDC的面积![]() DC×EG
DC×EG![]()
![]() ×(
×(![]() )=
)=![]() .
.
故答案为:![]() .
.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
【题目】“节能环保”是对美好家园的一种守护,某汽车制造厂生产一种新型能源汽车,计划半年后每月生产汽车20辆,由于另有任务,每月上班人数不一定相等,实际每月生产量与计划量相比情况如下表(增加为正,减少为负):
月份 | 一 | 二 | 三 | 四 | 五 | 六 |
增减(辆) | +3 | -2 | -1 | +4 | +2 | -5 |
(1)生产量最多的一个月,比生产量最少的一个月多生产多少辆?
(2)半年内总生产量是多少?比计划多了还是少了?多或少多少辆?