题目内容
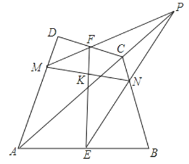
【题目】如图，四边形中ABCD中，E，F分别是AB，CD的中点，P为对角线AC延长线上的任意一点，PF交AD于M，PE交BC于N，EF交MN于K．
求证：K是线段MN的中点．
【答案】证明见解析.
【解析】
取AC的中点Q，连接QF、QE，过C点作CR∥QF交MP于点R，连接NR．由QF∥AD，QE∥NC可证得
=
．由CR∥AD可知
=
=1，则
==，从而可证得FK∥RN，最后可得KM=KN．
取AC的中点Q，连接QF、QE，过C点作CR∥QF交MP于点R，连接NR，
∵Q、F、E分别是AC、CD、AB的中点，
∴QF∥AD，QE∥NC，
∴=
，
=，
∵AQ=CQ，
∴=,
∵QF∥AD，CR∥QF，
∴CR∥AD，
∴==1，
∴FM=FR，
∴==，
∴EF∥RN．
∵FK∥RN，FM=FR，
∴KM=KN，即K是线段MN的中点．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
【题目】某家具商场计划购进某种餐桌、餐椅进行销售，有关信息如下表：
原进价（元/张） | 零售价（元/张） | 成套售价（元/套） | |
餐桌 | a | 270 | 500 |
餐椅 | b | 70 |
若购进3张餐桌18张餐椅需要1170元；若购进5张餐桌25张餐椅需要1750元．
（1）求表中a，b的值；
（2）若该商场购进餐椅的数量是餐桌数量的5倍还多20张，且餐桌和餐椅的总数量不超过200张．该商场计划将全部餐桌配套销售（一张餐桌和四张餐椅配成一套），其余餐椅以零售方式销售．设购进餐桌的数量为x（张），总利润为W（元），求W关于x的函数关系式，并求出总利润最大时的进货方案．
