题目内容
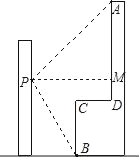
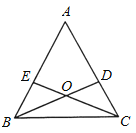
【题目】如图所示,已知在△ABC中,AB=AC,BD和CE分别是∠ABC和∠ACB的角平分线,且BD和CE相交于O点.
(1)试说明△OBC是等腰三角形;
(2)连接OA,试判断直线OA与线段BC的关系,并说明理由.
【答案】(1)详见解析;(2)直线AO垂直平分BC
【解析】
(1)根据对边对等角得到∠ABC=∠ACB,再结合角平分线的定义得到∠OBC=∠OCB,从而证明OB=OC;
(2)首先根据全等三角形的判定和性质得到OA平分∠BAC,再根据等腰三角形的三线合一的性质得到直线AO垂直平分BC.
(1)∵ 在△ABC中,AB=AC,
∴ ∠ABC=∠BCA,
∵ BD、CE分别平分∠ABC、∠BCA,
∴ ∠ABD=∠CBD ,∠ACE=∠BCE,
∴ ∠OBC=∠BCO,
∴ OB=OC,
∴ △OBC为等腰三角形;
(2)在△AOB与△AOC中,
∵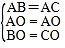 ,
,
∴△AOB≌△AOC(SSS),
∴∠BAO=∠CAO,∴直线AO垂直平分BC.(等腰三角形顶角的平分线、底边上的高、底边上的中线互相重合)

练习册系列答案
相关题目
【题目】现有A、B两种手机上网计费方式,收费标准如下表所示:
计费方式 | 月使用费/元 | 包月上网时间/分 | 超时费/(元/分) |
A | 30 | 120 | 0.20 |
B | 60 | 320 | 0.25 |
设上网时间为x分钟,
(1)若按方式A和方式B的收费金额相等,求x的值;
(2)若上网时间x超过320分钟,选择哪一种方式更省钱?