题目内容
【题目】已知,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,过点E作EF∥BC交直线AB于点F,连接CF.
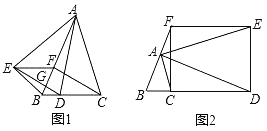
(1)如图1,点D在BC上,AB与DE交于点G,连接BE.求证:四边形DCFE是平行四边形;
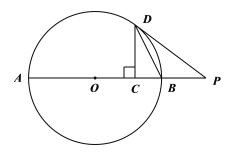
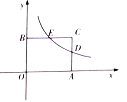
(2)如图2,点D在BC的延长线上,若四边形CDEF是矩形,AC=7,BC=4,求AE的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由SAS证明△ACD≌△ABE得出CD=BE,∠ACD=∠ABE,由平行线的性质得出∠ABC=∠EFB,得出∠ABE=∠EFB,证出EB=EF,得出EF=CD,即可得出结论;
(2)证出∠ACF=∠AFC,得出AF=AC=7,BF=7+7=14,由勾股定理得出CF=DE=6![]() ,证明△ABC∽△ADE,利用相似三角形的对应边成比例得出比例式即可求得答案.
,证明△ABC∽△ADE,利用相似三角形的对应边成比例得出比例式即可求得答案.
(1)∵∠BAC=∠DAE,
∴∠DAC=∠EAB,
在△ACD和△ABE中,
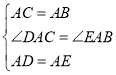 ,
,
∴△ACD≌△ABE(SAS),
∴CD=BE,∠ACD=∠ABE,
∵EF∥BC,
∴∠ABC=∠EFB,
∴∠ABE=∠EFB,
∴EB=EF,
∴EF=CD,
∵EF∥BC,
∴四边形EDCF是平行四边形;
(2)∵四边形CDEF为矩形,
∴∠BCF=90°,
∵AB=AC,
∴∠B=∠ACB,
∴∠ACF=∠AFC,
∴AF=AC=7,BF=7+7=14,
∴DE=CF=![]() ,
,
∵AB=AC,AD=AE,
∴![]() ,
,
∵∠BAC=∠DAE,
∴△ABC∽△ADE,
∴![]() ,
,
∴![]() ,
,
解得:AE=![]() .
.

【题目】某商场用36万元购进A、B两种商品,销售完后共获利6万元,其进价和售价如下表:
A | B | |
进价(元/件) | 1200 | 1000 |
售价(元/件) | 1380 | 1200 |
(注:获利=售价-进价)
(1) 该商场购进A、B两种商品各多少件?
(2) 商场第二次以原进价购进A、B两种商品.购进B种商品的件数不变,而购进A种商品的件数是第一次的2倍,A种商品按原价出售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81600元,B种商品最低售价为每件多少元?