ЬтФПФкШн
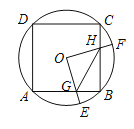
ЁОЬтФПЁПШчЭМЃЌОиаЮOABCЕФЖЅЕуAЃЌCдкxЃЌyжсе§АыжсЩЯЃЌЗДБШР§КЏЪ§![]() Й§OBЕФжаЕуDЃЌгыBCЃЌABНЛгкM,NЃЌЧввбжЊD(m,2),N(8,n)ЃЎ
Й§OBЕФжаЕуDЃЌгыBCЃЌABНЛгкM,NЃЌЧввбжЊD(m,2),N(8,n)ЃЎ
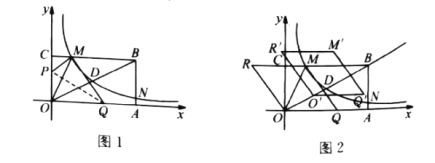
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєНЋОиаЮвЛНЧелЕўЃЌЪЙЕуOгыЕуMжиКЯЃЌелКлЮЊPQЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌШєНЋ![]() биOMЯђзѓЗелЃЌЕУЕНСтаЮOQMRЃЌНЋИУСтаЮбиЩфЯпOBвдУПУы
биOMЯђзѓЗелЃЌЕУЕНСтаЮOQMRЃЌНЋИУСтаЮбиЩфЯпOBвдУПУы![]() ИіЕЅЮЛЯђЩЯЦНвЦtУыЃЎ
ИіЕЅЮЛЯђЩЯЦНвЦtУыЃЎ
Ђй гУtЕФДњЪ§ЪНБэЪО![]() КЭ
КЭ![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
Ђк вЊЪЙИУСтаЮЪМжегыЗДБШР§КЏЪ§ЭМЯёгаНЛЕуЃЌЧѓtЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉЂй
ЃЛЃЈ3ЃЉЂй![]() ЃЛ
ЃЛ![]() ЃЛЂк
ЃЛЂк ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтЕУOA=8ЃЌвђЮЊDЮЊOBЕФжаЕуЃЌЕУГіDЃЈ4ЃЌ2ЃЉЃЌДњШыЗДБШР§КЏЪ§ЕФНтЮіЪНПЩЕУЃЛ
ЃЈ2ЃЉЧѓГіMЕуЕФзјБъЃЌдйРћгУЙДЙЩЖЈРэЧѓГіOPЕФГЄЃЌПЩЕУЕуPзјБъЃЛ
ЃЈ3ЃЉЂйЙ§ЕуOЁфзїOЁфTЁЭxжсЃЌДЙзуЮЊTЃЌПЩЕУЁїOOЁфTЁзЁїOBAЃЌНјЖјПЩБэЪО![]() ЕФзјБъЃЌРћгУЙДЙЩЖЈРэЧѓГіCRЃЌПЩБэЪО
ЕФзјБъЃЌРћгУЙДЙЩЖЈРэЧѓГіCRЃЌПЩБэЪО![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЂкАбRЁфЃЈ2t-3ЃЌt+4ЃЉДњШыЗДБШР§КЏЪ§ЕФНтЮіЪННтД№МДПЩЃЎ
НтЃКЃЈ1ЃЉЁпNЃЈ8ЃЌnЃЉЃЌЫФБпаЮOABCЪЧОиаЮЃЌ
ЁрOA=8ЃЌ
ЁпDЮЊOBЕФжаЕуЃЌ
ЁрDЃЈ4ЃЌ2ЃЉЃЌ
Ёр2=![]() ЃЌдђk=8ЃЌ
ЃЌдђk=8ЃЌ
Ёрy=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁпDЃЈ4ЃЌ2ЃЉЃЌ
ЁрЕуMзнзјБъЮЊ4ЃЌ
Ёр4=![]() ЃЌдђx=2ЃЌ
ЃЌдђx=2ЃЌ
ЁрMЃЈ2ЃЌ4ЃЉЃЌ
ЩшOP=xЃЌдђMP=xЃЌCP=4-xЃЌCM=2ЃЌгЩЙДЙЩЖЈРэЕУЃКЃЈ4-xЃЉ2+22=x2ЃЌ
НтЕУЃКx=![]() ЃЌМДOP=
ЃЌМДOP=![]() ЃЌ
ЃЌ
ЁрPЃЈ0ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉЂйЙ§ЕуOЁфзїOЁфTЁЭxжсЃЌДЙзуЮЊTЃЎ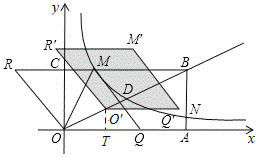
ПЩЕУЁїOOЁфTЁзЁїOBAЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() =
=![]() ЃЌ
ЃЌ
ЁпOOЁф=![]() ЃЌ
ЃЌ
ЁрOT=2tЃЌOЁфT=tЃЌ
ЁрOЁфЃЈ2tЃЌtЃЉЃЛ
ЩшCR=xЃЌдђOR=RM=x+2ЃЌ
Ёрx2+42=ЃЈx+2ЃЉ2ЃЌНтЕУx=3ЃЌМДCR=3ЃЌ
ЁрRЁфЃЈ2t-3ЃЌt+4ЃЉЃЛ
ЂкЁпRЁфЃЈ2t-3ЃЌt+4ЃЉЃЌ
ИљОнЬтвтЕУЃКt+4=![]() ЃЌ
ЃЌ
ЛЏМђЕУЃК2t2+5t-20=0ЃЌ
НтЕУЃК![]() Лђ
Лђ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
![]()