题目内容
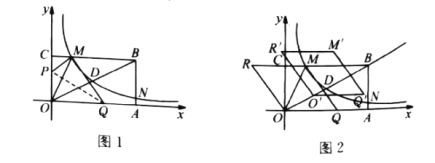
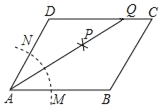
【题目】如图，在平行四边形ABCD中，按以下步骤作图：①以A为圆心，任意长为半径作弧，分别交AB，AD于点M，N；②分别以M，N为圆心，以大于
MN长为半径作弧，两弧相交于点P；③作射线AP，交边CD于点Q，若DC＝3QC，BC＝6，则平行四边形ABCD周长为_____．
【答案】30
【解析】
根据角平分线的性质可知∠DAQ=∠BAQ，再由平行四边形的性质得出CD∥AB，BC=AD=6，∠BAQ=∠DQA，故可得出△AQD是等腰三角形，据此可得出DQ=AD，进而可得出结论．
∵由题意可知，AQ是∠DAB的平分线，
∴∠DAQ=∠BAQ．
∵四边形ABCD是平行四边形，
∴CD∥AB，BC=AD=6，∠BAQ=∠DQA，
∴∠DAQ=∠DQA，
∴△AQD是等腰三角形，
∴DQ=AD=6．
∵DC=3QC，
∴QC=
DQ=3，
∴CD=DQ+CQ=6+3=9，
∴平行四边形ABCD周长=2（DC+AD）=2×（9+6）=30．
故答案为：30．
练习册系列答案
阅读快车系列答案
相关题目
