题目内容
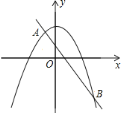
【题目】如图,抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(2,q)两点,则不等式ax2+mx+c>n的解集是( )
A.-1<x<2B.x>-1或x<2C.-2<x<1D.x<-2或x>1
【答案】C
【解析】
作直线y=mx+n关于y轴的对称直线CD:y=mx+n,交抛物线y=ax2+c于C、D两点,根据点的的对称性,可知点C(1,p),D(2,q),求不等式ax2+mx+c>n的解集,也就是求不等式ax2+c>mx+n的解集,由图即可求解.
解:作直线y=mx+n关于y轴的对称直线CD:y=mx+n,
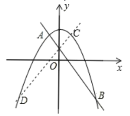
点C、D是两个函数的交点,根据点的的对称性,点C(1,p),D(2,q),
由图象可以看出,ax2+mx+c>n的解集为:2<x<1,
故选C.

练习册系列答案
相关题目
【题目】“鲜乐”水果店购进一优质水果,进价为 10 元/千克,售价不低于 10 元/千克,且不超过 16 元/千克,根据销售情况,发现该水果一天的销售量 y(千克) 与该天的售价 x(元/千克)满足如下表所示的一次函数关系
销售量 y(千克) | … | 29 | 28 | 27 | 26 | … |
售价 x(元/千克) | … | 10.5 | 11 | 11.5 | 12 |
(1)某天这种水果的售价为 14 元/千克,求当天该水果的销售量;
(2)如果某天销售这种水果获利 100 元,那么该天水果的售价为多少元?