题目内容
【题目】大学生小亮响应国家创新创业号召，回家乡承包了一片坡地，改造后种植优质称猴桃．经核算这批称猴桃的种植成本为16元/kg．设销售时间为x（天），通过一个月（30天）的试销得出如下规律：
①称猴桃的销售价格p（元/kg）与时间x（天）的关系：
当1≤x＜20时，p与x满足一次函数关系．如下表：
x（天） | 2 | 4 | 6 | … |
p（元/kg） | 35 | 34 | 33 | … |
当20≤x≤30时，销售价格稳定为24元/kg；
②称猴桃的销售量y（kg）与时间x（天）的关系：第一天卖出24kg，以后每天比前一天多卖出4kg．
（1）填空：试销的一个月中，销售价p（元/kg）与时间x（天）的函数关系式为 ；销售量y（kg）与时间x（天）的函数关系式为 ；
（2）求试售第几天时，当天的利润最大？最大利润是多少？
【答案】（1）p＝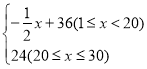
，y＝4x+24；（2）销售第30天时，利润最大，最大利润为1152元．
【解析】
（1）依据题意易得出销售价p（元/kg）与时间x（天）之间的函数关系式；
（2）然后根据销售利润=销售量x（售价-进价），列出平均每天的销售利润W（元）与时间x（天）之间的函数关系式，再依据函数的增减性求得最大利润.
解：（1）依题意，当1≤x＜20时，设p＝kx+b，得
，
解得p＝﹣
x+36，
故销售价p（元/kg）与时间x（天）的函数关系式为，p＝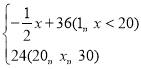
，
由②得，销售量y（kg）与时间x（天）的函数关系式为：y＝4x+24，
故答案为：p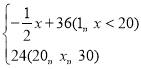＝ ，y＝4x+24；
（2）设利润为W，
①当1≤x＜20时，W＝（﹣x+36﹣16）（4x+24）
＝﹣2（x﹣17）2+1058
∴x＝17时，W最大＝1058，
②当20≤x≤30时，
W＝（24﹣16）（4x+24）
＝32x+192
∴x＝30时，W最大＝1152
∵1152＞1058
∴销售第30天时，利润最大，最大利润为1152元．
【题目】发散思维2017·丰台区二模为了解某校八年级学生每周上网的时间，两名学生进行了抽样调查，小丽调查了八年级电脑爱好者中40名学生每周上网的时间，小杰从全校400名八年级学生中随机抽取了40名学生，调查了他们每周上网的时间．小丽与小杰整理各自的样本数据，如下表所示：
时间段(时/周) | 小丽抽样人数 | 小杰抽样人数 |
0～1 | 6 | 22 |
1～2 | 10 | 10 |
2～3 | 16 | 6 |
3～4 | 8 | 2 |
(表中每组数据包含最小值，不包含最大值)
(1)你认为哪名同学抽取的样本不合理？请说明理由；
(2)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间，估计该校全体八年级学生中有多少名学生应适当减少上网的时间．
