题目内容
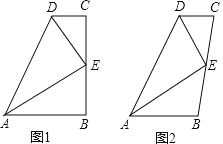
【题目】如图,在△ABC 中,∠BAC=90°,AB=AC,D 是 AC 边上一动点, CE⊥BD 于 E.
(1)如图(1),若 BD 平分∠ABC 时,①求∠ECD 的度数;②求证:BD=2EC;
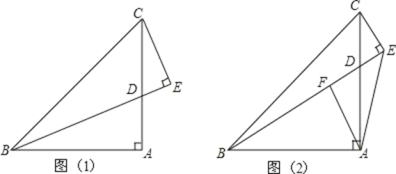
(2)如图(2),过点 A 作 AF⊥BE 于点 F,猜想线段 BE,CE,AF 之间的数量关系并证明你的猜想.
【答案】(1)①22.5°;②见解析;(2) BE﹣CE=2AF,理由见解析.
【解析】
(1)①根据等腰直角三角形的性质得出∠CBA=45![]() ,再利用角平分线的定义解答即可;
,再利用角平分线的定义解答即可;
②延长CE交BA的延长线于点G得出CE=GE,再利用AAS证明ΔABD≌ΔACG,利用全等三角形的性质解答即可;
(2)过点A作AH⊥AE,交BE于点H,证明ΔABH≌ΔACE,进而得出CE=BH,利用等腰直角三角形的判定和性质解答即可.
解:(1)①∵在△ABC 中,∠BAC=90°,AB=AC,
∴∠CBA=45°,
∵BD 平分∠ABC,
∴∠DBA=22.5°,
∵CE⊥BD,
∴∠ECD+∠CDE=90°,∠DBA+∠BDA=90°,
∵∠CDE=∠BDA,
∴∠ECD=∠DBA=22.5°;
②延长 CE 交 BA 的延长线于点 G,如图 1:

∵BD 平分∠ABC,CE⊥BD,
∴CE=GE,
在△ABD 与△ACG 中,
 ,
,
∴△ABD≌△ACG(AAS),
∴BD=CG=2CE;
(2)结论:BE﹣CE=2AF.
过点 A 作 AH⊥AE,交 BE 于点 H,如图 2:

∵AH⊥AE,
∴∠BAH+∠HAC=∠HAC+∠CAE,
∴∠BAH=∠CAE,
在△ABH 与△ACE 中,
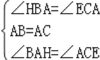
∴△ABH≌△ACE(ASA),
∴CE=BH,AH=AE,
∴△AEH 是等腰直角三角形,
∴AF=EF=HF,
∴BE﹣CE=2AF.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案【题目】为了给游客提供更好的服务,某景区随机对部分游客进行了关于“景区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.
满意度 | 人数 | 所占百分比 |
非常满意 | 12 | 10% |
满意 | 54 | m |
比较满意 | n | 40% |
不满意 | 6 | 5% |

根据图表信息,解答下列问题:
(1)本次调查的总人数为______,表中m的值为_______;
(2)请补全条形统计图;
(3)据统计,该景区平均每天接待游客约3600人,若将“非常满意”和“满意”作为游客对景区服务工作的肯定,请你估计该景区服务工作平均每天得到多少名游客的肯定.