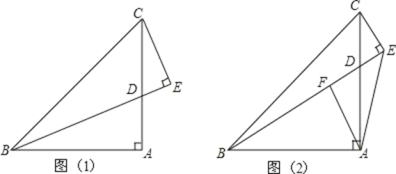
题目内容
【题目】已知AB=AC,D,E是BC边上的点,将△ABD绕点A旋转,得到△ACD',连接D'E.

(1)如图①,当∠BAC=120°,∠DAE=60°时,求证DE=D'E.
(2)如图②,当DE=D'E时,∠DAE与∠BAC有怎样的数量关系?请写出,并说明理由.
【答案】(1)详见解析;(2)∠DAE=![]() ∠BAC,理由详见解析.
∠BAC,理由详见解析.
【解析】
(1)根据旋转的性质和全等三角形的判定定理SAS证得△DAE≌△D′AE,则由“全等三角形的对应边相等”的性质证得结论;
(2)∠DAE=![]() ∠BAC.根据旋转的性质和全等三角形的判定定理SSS证得△DAE≌△D′AE,则由“全等三角形的对应角相等”的性质推知∠DAE=
∠BAC.根据旋转的性质和全等三角形的判定定理SSS证得△DAE≌△D′AE,则由“全等三角形的对应角相等”的性质推知∠DAE=![]() ∠BAC.
∠BAC.
(1)证明:如图,

∵△ABD旋转得到△ACD',
∴∠DAD'=∠BAC=120°,AD=AD'.
∵∠DAE=60°,
∴∠EAD'=∠DAD'-∠DAE=120°-60°=60°.
∴∠DAE=∠D'AE,
又∵AE=AE,AD=AD',
∴△DAE≌△D'AE(SAS).
∴DE=D'E.
(2)解:∠DAE=![]() ∠BAC.
∠BAC.
理由:如图,
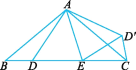
∵△ABD旋转得到△ACD',
∴∠DAD'=∠BAC,AD=AD'.
∵DE=D'E,AE=AE,
∴△DAE≌△D'AE(SSS).
∴∠DAE=D'AE=![]() ∠DAD'.
∠DAD'.
∴∠DAE=![]() ∠BAC.
∠BAC.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案【题目】为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
某校九年级50名学生跳高测试成绩的频数表
组别(m) | 频数 |
1.09~1.19 | 8 |
1.19~1.29 | 12 |
1.29~1.39 | A |
1.39~1.49 | 10 |

(1)求A的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.