Question

【题目】如图所示，抛物线的图象过，，三点，顶点为．

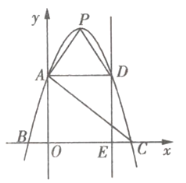
(1)求抛物线的解析式；

(2)设点在轴上，且，求的长；

(3)若轴且在抛物线上，过作于，在直线上运动，点在轴上运动，是否存在这样的点、使以、、为顶点的三角形与相似?若存在，请求出点、的坐标．

Answer 1

【答案】(1)；(2)或5； (3)存在三组点：①或②或③．

【解析】

（1）利用待定系数法求函数解析式；

（2）根据AO=CO=3得到∠OGB+∠OAB=45°，过作交延长线于，证得△BHG是等腰直角三角形，，再证明求出， ，即可求出AG；

（3）根据点A、P、D的坐标得到△PAD为等腰直角三角形，分∠AMN、∠ANM、∠MAN是直角，夹直角的两边相等，分别求出点M、N的坐标即可.

(1)由可另设解析式为.

把代入，得，

，

；

(2)，

.

过作交延长线于.

是等腰直角三角形，.

又，

.

.

又，

，

同理，当点G在y轴正半轴时，可得AG＝1，

或5；

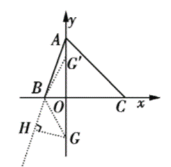
(3)由题意得：顶点.

为等腰直角三角形.

∴只要也是等腰直角三角形，两个三角形就相似.

①如图1所示，，

可得.

.

；

②如图2所示，，

可得.

，

；

③如图3所示，，

可得.

，

；

④如图4所示，若，

则，但，

∴不存在，

综上，存在三组点：①或②或③.