Question

【题目】已知抛物线：=（为任意实数）

（1）无论取何值，抛物线恒过两点________，________．

（2）当时，设抛物线在第一象限依次经过整数点（横、纵坐标均为整数的点）为，…．将抛物线沿直线平移，平移后的抛物线记为，抛物线经过点，的顶点为（，例如时，抛物线经过点，顶点为）

①抛物线的解析式为________；顶点坐标为________；

②在抛物线上是否存在点，使得？若存在，求出点的坐标，并判断四边形的形状；若不存在，请说明理由．

③直接写出线段的长________．

Answer 1

【答案】（1），；（2）①，；②存在，点坐标为；是矩形；③

【解析】

（1）由抛物线C的解析式，令的系数为0，得出的值，进而求出抛物线恒过的点的坐标；

（2）①当时，抛物线C可化简为，根据题意，格点(2,4)，根据抛物线平移的性质，可设平移后的抛物线为（m＞0），将(2,4)代入，即可得解；

②用待定系数法求出抛物线和直线解析式，假设存在点，使得，求出直线，联立直线和抛物线，即可求出P点坐标；根据两点间距离公式求出和，再结合勾股定理逆定理求出∠=90°，即可判定四边形为矩形；

③由题意可设，将其代入平移后的抛物线（m＞0），求出m=2n-1，于是，同理得出，由两点间距离公式即可得解．

（1）=

令，

解得或

将代入抛物线C的解析式，得，

将代入抛物线C的解析式，得，

∴无论取何值，抛物线恒过两点，，

故答案为，；

（2）①当时，抛物线C：，

根据题意，A1(1,1)，A2(2,4)，

设平移后的抛物线为（m＞0），

代入A2(2,4)，得抛物线C2：

解得，m=0（舍）或m=3

∴抛物线的解析式为，顶点坐标为(3,3)．

故答案为：，；

②将A1(1,1)代入（m＞0），

得

解得，m=0（舍）或m=1

∴抛物线：，顶点坐标

设直线的解析式为：

分别将A2(2,4)和M2(3,3)代入得

，解得

∴直线：

假设存在点，使得，

设直线为，

将代入得，解得：t=2，

所以直线：

联立，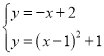

解得或（此点为M1）

∴存在点，使得，点坐标为；

∵，，

∴=，

又，

∴四边形是平行四边形，

又∵，，，

∴

∴∠=90°，

∴四边形是矩形；

③设，将其代入平移后的抛物线（m＞0），

解得m=2n-1，于是，

同理可得：，

∴，

故答案为：．