��Ŀ����
����Ŀ�����κ���y=��m+2��x2��2��m+2��x��m+5������m+2��0��
��1����ö��κ����ĶԳ��᷽�̣�
��2��������C��0��n����ֱ��l��y�ᣮ �ٵ�ֱ��l��������ֻ��һ��������ʱ����n��m�ĺ�����ϵ��
������������x�����������㣬����������x���·��IJ�����x�ᷭ�ۣ�ͼ������ಿ�ֱ��ֲ��䣬�õ�һ���µ�ͼ��n=7ʱ��ֱ��l���µ�ͼ��ǡ�������������㣬���ʱm��ֵ��
��3��������ÿһ��������x��ֵ��������Ӧ�ĺ���ֵ����С��1����m��ȡֵ��Χ�� 
���𰸡�
��1���⣺��y=��m+2��x2��2��m+2��x��m+5=��m+2����x��1��2��2m+3��
��Գ��᷽��Ϊx=1
��2���⣺����ͼ��������ֱ֪��l�Ľ���ʽΪy=n��
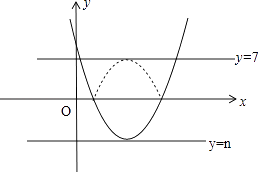
��ֱ��l��������ֻ��һ�������㣬
��n=��2m+3��
�������֪������2m+3=��7ʱ��ֱ��l���µ�ͼ��ǡ�������������㣮
��m=5
��3���⣺������y=��m+2��x2��2��m+2��x��m+5�Ķ��������ǣ�1����2m+3����
����ɵ� ![]() ���
��� ![]()
��m��ȡֵ��Χ�ǩ�2��m��1
����������1���������߽���ʽ�䷽�ɶ���ʽ���ɵã���2���ٻ��������Ĵ���ͼ����ͼ��ֱ֪��l��������ʽʱ��ֱ��l��������ֻ��һ�����㣬�ݴ˿ɵã��ڻ������ۺ���ͼ����ֱ��l���µ�ͼ��ǡ��������������ɵé�2m+3=��7����֮�ɵã���3���ɿ������ϼ�����ֵ����С��1�ɵ� ![]() ����֮���ɣ�
����֮���ɣ�
�����㾫����������Ĺؼ�����������κ���ͼ���ƽ�Ƶ����֪ʶ������ƽ�Ʋ��裺��1���䷽ y=a(x-h)2+k��ȷ�����㣨h,k����2����x������Ҽ�����y���ϼ��¼����Լ�����������������Ľ�������⣬�˽�һԪ���η��̵Ľ������Ӧ�Ķ��κ�����ͼ����x��Ľ������꣮���һԪ���η����е�b2-4ac���ڶ��κ����б�ʾͼ����x���Ƿ��н��㣮��b2-4ac>0ʱ��ͼ����x�����������㣻��b2-4ac=0ʱ��ͼ����x����һ�����㣻��b2-4ac<0ʱ��ͼ����x��û�н��㣮

����Ŀ��ij����С��Ϊ���˽��������ο������ڹ���ƿװ���������������һ�죬���Ƿֱ���A��B��C�������ڴ����뿪�����οͽ��е��飬������A���ڵ������õ�������������������ͼ��ʾ��ͳ��ͼ��

(1)��A���ڵı������ο��У�����2ƿ��2ƿ�������ϵ��ο�����ռA���ڵı������ο�������______%��
(2)���ʣ�A���ڵı������ο��������˾������˶���ƿ���ϣ�
(3)��֪B��C�������ڵı������ο��������˾��������ϵ��������±���ʾ��
���� | B | C |
�˾�������������(ƿ) | 3 | 2 |
��C���ڵı�����������B���ڵı�����������2���ˣ���B��C�������ڵı������ο������ڹ�������49��ƿ���ϣ����ʣ�B���ڵı������ο��ж������ˣ�