题目内容
【题目】如图,四边形ABCD中,AB=AD=2,∠A=60°,BC=![]() ,CD=3.
,CD=3.

(1)求∠ADC的度数;
(2)求四边形ABCD的面积.
【答案】(1)150°;(2)![]()
【解析】
(1)连接BD,由一个角是60°的等腰三角形是等边三角形可判定△ABD为等边三角形,然后由勾股定理逆定理判定△BCD为直角三角形,即可求出∠ADC;
(2)分别计算等边三角形面积和直角三角形面积求和即可.
解:(1) 连接BD
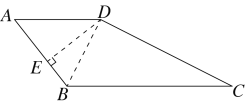
∵∠A=60°,AB=AD,∴△ABD为等边三角形
∴BD=AB=2,
∴BD2+CD2=4+9=13,BC2=13, ∴BD2+CD2=13=BC2,
∴∠BDC=90°,∴∠ADC=90° + 60°=150°
(2)作DE⊥AB于E,则∠DEB=90°,∴BE=1, ![]() ,
,
∴S四边形ABCD= S△DBC + S△ABD =![]() ×2×3+
×2×3+![]() ×2×
×2×![]() =
=![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某公司购进一种商品的成本为30元/kg,经市场调研发现,这种商品在未来90天的销售单价p(元/kg)与时间t(天)之间的相关信息如图,销售量y(kg)与时间t(天)之间满足一次函数关系,且对应数据如表,设第t天销售利润为w(元)
时间t(天) | 10 | 30 |
每天的销售量 y(kg) | 180 | 140 |
(1)分别求出售单价p(元/kg)、销售量y(kg)与时间t(天)之间的函数关系式;
(2)问:销售该商品第几天时,当天的销售利润最大?并求出最大利润;




