题目内容
如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=1,AB=3,BC=3,点P是AB上一个动点,则PC+PD的和最小值为 .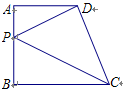

5
延长DA到D′,则D和D′关于AB对称,连接CD′,与AB相交于点P,
根据“两点之间线段最短”可得此时PC+PD的和最小.
由于AD′∥BC,则△APD′∽△BPC.
设PB=x,则AP=5-x.
所以 AP/BP= AD'/BC,
即 5-x/x=4/6
解得x=3,
即PB=3.
PC=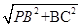 =
= 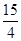
PD′=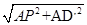 =
= 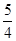
则PC+PD的和最小值为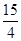 +
+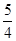 =5
=5
根据“两点之间线段最短”可得此时PC+PD的和最小.
由于AD′∥BC,则△APD′∽△BPC.
设PB=x,则AP=5-x.
所以 AP/BP= AD'/BC,
即 5-x/x=4/6
解得x=3,
即PB=3.
PC=
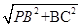 =
= 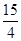
PD′=
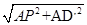 =
= 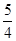
则PC+PD的和最小值为
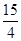 +
+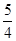 =5
=5
练习册系列答案
相关题目
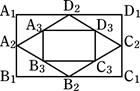
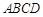 中,
中,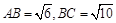 .第一次将纸片折叠,使点
.第一次将纸片折叠,使点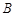 与点
与点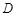 重合,折痕与
重合,折痕与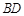 交于点
交于点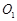 ;设
;设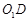 的中点为
的中点为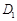 ,第二次将纸片折叠使点
,第二次将纸片折叠使点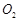 ;设
;设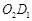 的中点为
的中点为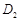 ,第三次将纸片折叠使点
,第三次将纸片折叠使点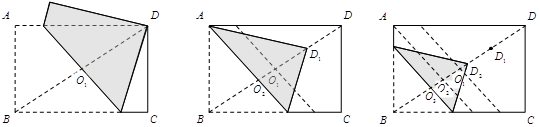
 ABCD,E是BA延长线上一点,AB=AE,连接CE交AD于点F,若CF平分∠BCD,AB=3,则BC的长为 .
ABCD,E是BA延长线上一点,AB=AE,连接CE交AD于点F,若CF平分∠BCD,AB=3,则BC的长为 .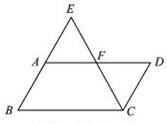
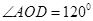 ,AB=2.5,则AC的长为 。
,AB=2.5,则AC的长为 。
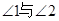 满足 关系时AB//CD,(只要写出一个你认为成立的条件)。
满足 关系时AB//CD,(只要写出一个你认为成立的条件)。