题目内容
【题目】某课外学习小组根据学习函数的经验,对函数y=x3﹣3x的图象与性质进行了探究.请补充完整以下探索过程:
(1)列表:
x | … | ﹣2 |
| ﹣1 |
| 0 |
| 1 |
| 2 | … |
y | … | ﹣2 | m | 2 |
| 0 |
| n |
| 2 | … |
请直接写出m,n的值;
(2)根据上表中的数据,在平面直角坐标系内补全该函数的图象;
(3)若函数y=x3﹣3x的图象上有三个点A(x1,y1),B(x2,y2),C(x3,y3),且x1<﹣2<x2<2<x3,则y1,y2,y3之间的大小关系为 (用“<”连接);
(4)若方程x3﹣3x=k有三个不同的实数根.请根据函数图象,直接写出k的取值范围.
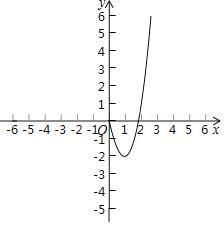
【答案】(1)m=![]() ,n=﹣2;(2)见解析;(3)y1<y2<y3;(4)﹣2<k<2.
,n=﹣2;(2)见解析;(3)y1<y2<y3;(4)﹣2<k<2.
【解析】
(1)从函数的对称性可得:m=![]() ,n=﹣2;
,n=﹣2;
(2)描点如下函数图象;
(3)从图象看,确定x1、x2、x3,再图象上的位置,即可求解;则y1,y2,y3之间的大小关系为:y1<y2<y3;
(4)方程x3﹣3x=k有三个不同的实数根,从图象即可看出.
解:(1)从函数的对称性可得:m=![]() ,n=﹣2;
,n=﹣2;
(2)描点如下函数图象
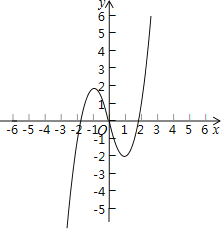
(3)从图象看,x1<﹣2<x2<2<x3,则y1,y2,y3之间的大小关系为:y1<y2<y3,
故答案为:y1<y2<y3;
(4)从图象看,方程x3﹣3x=k有三个不同的实数根,在x轴下方的临界点是y=﹣2,同理x轴上方的临界点是y=2,故:﹣2<k<2.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目