题目内容
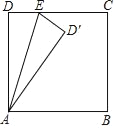
【题目】如图,长方形ABCD中,∠A=∠ABC=∠BCD=∠D=90°,AB=CD=5,AD=BC=13,点E为射线AD上的一个动点,若△ABE与△A'BE关于直线BE对称,当△A'BC为直角三角形时,AE的长为__.

【答案】1或25.
【解析】
分点E在线段AD上,点E在线段AD的延长线上两种情况讨论,由题意可得AB=A'B=5,∠EA'B=90°,AE=A'E,A'C=12,根据勾股定理和全等三角形的性质,可求AE的长.
解:若点E在线段AD上,
∵若△ABE与△A′BE关于直线BE对称,
∴AB=A'B=,5,∠EA'B=90°,AE=A'E
∵△A'BC为直角三角形
∴∠BA'C=90°
∴A'C=![]() =
=![]() =12,
=12,
∵∠EA'B=90°,∠BA'C=90°
∴∠CA'E=180°
∴点E,点C,点A'共线
在Rt△CDE中,DC2+DE2=CE2.
∴(A'E+12)2=(13﹣AE)2+25,
∴AE=1,
若点E在线段AD的延长线上,且点C在A'E上,如图所示:
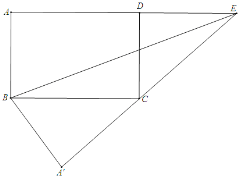
∵△ABE与△A′BE关于直线BE对称,
∴AB=A'B=,5,∠A=∠A'=90°
在Rt△A'BC中,A'C=![]() =
=![]() =12,
=12,
∵∠BCA'+∠DCE=90°,∠DCE+∠DEC=90°
∴∠BCA'=∠DEC,
∵∠A'=∠EDC=90°,AB=CD=A'B,
∴在△A'C和△DCE中,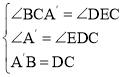 ,
,
∴△A'BC≌△DCE(AAS),
∴DE=A'C=12,
∴AE=1AD+DE=13+12=25;
故答案为:1或25.

练习册系列答案
相关题目