题目内容
【题目】如图,矩形ABCD中,AD=10,AB=8,点E为边DC上一动点,连接AE,把△ADE沿AE折叠,使点D落在点D′处,当△DD′C是直角三角形时,DE的长为_____.
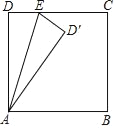
【答案】4或5.
【解析】
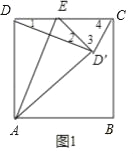

∵△ADE沿AE折叠,使点D落在点D′处,
∴DE=D′E,AD=AD′=10,
(1)当∠DD′C=90°时,如图1,
∵DE=D′E,
∴∠1=∠2,
∵∠1+∠4=90°,∠2+∠3=90°,
∴∠3=∠4,
∴ED′=EC,
∴DE=EC=![]() CD=4;
CD=4;
(2)当∠DCD′=90°时,则点D′落在BC上,如图2,
设DE=x,则ED′=x,CE=8﹣x,
∵AD′=AD=10,
∴在Rt△ABD′中,BD′=![]() =6,
=6,
∴CD′=4,
在Rt△CED′中,(8﹣x)2+42=x2,解得x=5,
即DE的长为5,
综上所述,当△DD′C是直角三角形时,DE的长为4或5.
故答案为4或5.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目






