题目内容
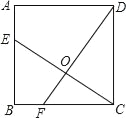
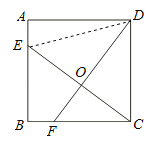
【题目】如图,正方形ABCD的边长为4,点E、F分别在AB、BC上,且AE=BF=1,CE、DF交于点O,下列结论:①∠DOC=90°,②OC=OE,③CE=DF,④tan∠OCD=![]() ,⑤S△DOC=S四边形EOFB中,正确的有( )
,⑤S△DOC=S四边形EOFB中,正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】分析:由正方形ABCD的边长为4,AE=BF=1,利用SAS易证得△EBC≌△FCD,然后全等三角形的对应角相等,易证得①∠DOC=90°正确,③CE=DF正确;②由线段垂直平分线的性质与正方形的性质,可得②错误;易证得∠OCD=∠DFC,即可求得④正确;由①易证得⑤正确.
详解:∵正方形ABCD的边长为4,∴BC=CD=4,∠B=∠DCF=90°.
∵AE=BF=1,∴BE=CF=4﹣1=3.
在△EBC和△FCD中,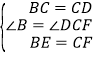 ,
,
∴△EBC≌△FCD(SAS),∴∠CFD=∠BEC,CE=DF,故③正确,
∴∠BCE+∠BEC=∠BCE+∠CFD=90°,∴∠DOC=90°;故①正确;
连接DE,如图所示,若OC=OE.
∵DF⊥EC,∴CD=DE.
∵CD=AD<DE(矛盾),故②错误;
∵∠OCD+∠CDF=90°,∠CDF+∠DFC=90°,∴∠OCD=∠DFC,∴tan∠OCD=tan∠DFC=![]() =
=![]() ,故④正确;
,故④正确;
∵△EBC≌△FCD,∴S△EBC=S△FCD,∴S△EBC﹣S△FOC=S△FCD﹣S△FOC,即S△ODC=S四边形BEOF.故⑤正确;
故正确的有:①③④⑤.
故选D.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目