题目内容
【题目】如图,直线y= ![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).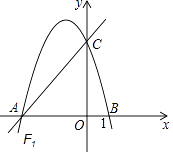
(1)求抛物线F1所表示的二次函数的表达式及顶点Q的坐标;
(2)在抛物线上是否存在点P,使△BPC的内心在y轴上,若存在,求出点P的坐标,若不存在写出理由;
(3)直线y=kx﹣6与y轴交于点N,与直线AC的交点为M,当△MNC与△AOC相似时,求点M坐标.
【答案】
(1)解:令y=0代入y= ![]() x+4,解得:x=﹣3,
x+4,解得:x=﹣3,
∴A(﹣3,0).
令x=0,代入y= ![]() x+4,得y=4,
x+4,得y=4,
∴C(0,4).
设抛物线F1的解析式为:y=a(x+3)(x﹣1),
把C(0,4)代入上式得,a=﹣ ![]() ,
,
∴y=﹣ ![]() x2﹣
x2﹣ ![]() x+4.
x+4.
∴y=﹣ ![]() (x2+2x+1)+
(x2+2x+1)+ ![]() ,
,
∴Q(﹣1, ![]() ).
).
(2)解:∵点B的坐标为(1,0),取点B关于y轴的对称点B′(﹣1,0),连接CB′,则∠BCO=∠B′CO,
∴△BPC的内心在y轴上.
设直线B′C的解析式为y=kx+b,将点B′和点C的坐标代入得: ![]() ,
,
解得:k=4,b=4.
∴直线B′C的解析式为y=4x+4,
将y=4x+4与y=﹣ ![]() x2﹣
x2﹣ ![]() x+4联立得:
x+4联立得: 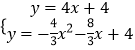 ,
,
解得: ![]() 或
或 ![]() (舍去).
(舍去).
∴点P的坐标为(﹣5,﹣16)
(3)解:N(0,﹣6),直线AC的表达式为y= ![]() x+4.
x+4.
当△MNC∽△AOC时,∠CMN=90°.
∴直线MN的一次项系数为﹣ ![]() .
.
∴MN的解析式为y=﹣ ![]() x﹣6.
x﹣6.
将y= ![]() x+4与y=﹣
x+4与y=﹣ ![]() x﹣6联立,解得:
x﹣6联立,解得: 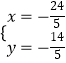 ,
,
∴点M的坐标为(﹣ ![]() ,﹣
,﹣ ![]() ).
).
②当∠CNM为直角时,MN∥x轴,
将y=﹣6代入y= ![]() x+4得:
x+4得: ![]() x+4=﹣6,解得:x=﹣
x+4=﹣6,解得:x=﹣ ![]() .
.
∴M(﹣ ![]() ,﹣6).
,﹣6).
综上所述,点M的坐标为(﹣ ![]() ,﹣
,﹣ ![]() )或(﹣
)或(﹣ ![]() ,﹣6)
,﹣6)
【解析】(1)先求得点A和点C的坐标,然后利用待定系数法求得二次函数的额解析式,接下来,利用配方法求得抛物线的顶点坐标即可;
(2)取点B关于y轴的对称点B′(-1,0),连接CB′,则∠BCO=∠B′CO,然后求得直线B′C的解析式为,然后将直线B′C的解析式与抛物线的解析式联立可求得点P的坐标;
(3)当∠CMN=90°时,先求得直线MN的解析式,然后将直线AC与直线MN的解析式联立可求得点点M的坐标;当∠CNM为直角时,MN∥x轴,再求得直线MN的解析式,然后将直线AC与直线MN的解析式联立可求得点点M的坐标.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200﹣2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.




