��Ŀ����
����Ŀ�����壺��ͼ1����M��N���߶�AB�ָ��AM��MN��BN������AM��MN��BNΪ�ߵ���������һ��ֱ�������Σ���Ƶ�M��N���߶�AB�Ĺ��ɷָ�㣮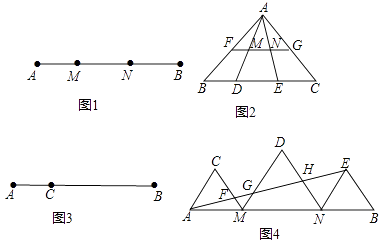
��1����֪��M��N���߶�AB�Ĺ��ɷָ�㣬��AM=2��MN=3����BN�ij���
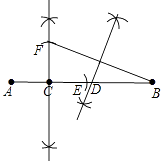
��2����ͼ2���ڡ�ABC�У�FG����λ�ߣ���D��E���߶�BC�Ĺ��ɷָ�㣬��EC��DE��BD������AD��AE�ֱ�FG�ڵ�M��N����֤����M��N���߶�FG�Ĺ��ɷָ�㣻
��3����֪��C���߶�AB�ϵ�һ���㣬��λ����ͼ3��ʾ������BC�ϻ�һ��D��ʹ��C��D���߶�AB�Ĺ��ɷָ�㣨Ҫ��߹���ͼ��������ͼ�ۼ�����һ�����μ��ɣ���
��4����ͼ4����֪��M��N���߶�AB�Ĺ��ɷָ�㣬MN��AM��BN����AMC����MND�͡�NBE��Ϊ�ȱ������Σ�AE�ֱ�CM��DM��DN�ڵ�F��G��H����H��DN���е㣬��̽��S��AMF �� S��BEN��S�ı���MNHG��������ϵ����˵�����ɣ�
���𰸡�
��1��
�ٵ�MNΪ����߶�ʱ��
�ߵ� M��N���߶�AB�Ĺ��ɷָ�㣬
��BN= ![]() =
= ![]() =
= ![]() ��
��
�ڵ�BNΪ����߶�ʱ��
�ߵ�M��N���߶�AB�Ĺ��ɷָ�㣬
��BN= ![]() =
= ![]() =
= ![]() ��
��
����������BN= ![]() ��
�� ![]()
��2��
֤������FG�ǡ�ABC����λ�ߣ�
��FG��BC��
�� ![]() =1��
=1��
���M��N�ֱ���AD��AE���е㣬
��BD=2FM��DE=2MN��EC=2NG��
�ߵ�D��E���߶�BC�Ĺ��ɷָ�㣬��EC��DE��BD��
��EC2=BD2+DE2��
�ࣨ2NG��2=��2FM��2+��2MN��2��
��NG2=FM2+MN2��
���M��N���߶�FG�Ĺ��ɷָ��
��3��
�⣺����������AB�Ͻ�ȡCE=CA��
����AE�Ĵ�ֱƽ���ߣ�����ȡCF=CA��
������BF������BF�Ĵ�ֱƽ���ߣ���AB��D��
��D��Ϊ������ͼ��ʾ��
��4��
�⣺S�ı���MNHG=S��AMF+S��BEN���������£�
��AM=a��BN=b��MN=c��
��H��DN���е㣬
��DH=HN= ![]() c��
c��
�ߡ�MND����BNE��Ϊ�ȱ������Σ�
���D=��DNE=60�㣬
�ڡ�DGH�͡�NEH�У�
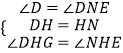 ��
��
���DGH�ա�NEH��ASA����
��DG=EN=b��
��MG=c��b��
��GM��EN��
���AGM�ס�AEN��
�� ![]() ��
��
��c2=2ab��ac+bc��
�ߵ� M��N���߶�AB�Ĺ��ɷָ�㣬
��c2=a2+b2��
�ࣨa��b��2=��b��a��c��
�֡�b��a��c��
��a=b��
�ڡ�DGH�͡�CAF�У�
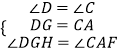 ��
��
���DGH�ա�CAF��ASA����
��S��DGH=S��CAF��
��c2=a2+b2��
�� ![]() c2=
c2= ![]() a2+
a2+ ![]() b2��
b2��
��S��DMN=S��ACM+S��ENB��
��S��DMN=S��DGH+S�ı���MNHG��S��ACM=S��CAF+S��AMF��
��S�ı���MNHG=S��AMF+S��BEN
����������1���ٵ�MNΪ����߶�ʱ���ɹ��ɶ������BN���ڵ�BNΪ����߶�ʱ���ɹ��ɶ������BN���ɣ���2����֤����M��N�ֱ���AD��AE���е㣬�ó�BD=2FM��DE=2MN��EC=2NG�����EC2=BD2+DE2 �� �ó�NG2=FM2+MN2 �� ���ɵó����ۣ���3����AB�Ͻ�ȡCE=CA����AE�㴹ֱƽ���ߣ���ȡCF=CA����BF�Ĵ�ֱƽ���ߣ���AB��D���ɣ���4����֤����DGH�ա�NEH���ó�DG=EN=b��MG=c��b����֤����AGM�ס�AEN���ó�����ʽ���ó�c2=2ab��ac+bc��֤��c2=a2+b2 �� �ó�a=b��֤����DGH�ա�CAF���ó�S��DGH=S��CAF �� ֤��S��DMN=S��ACM+S��ENB �� ���ɵó����ۣ�

����Ŀ���Ķ����²��ϣ�����Ҫ�������Ӧ������
�����У�ƽ���ı��Ρ����Ρ����Ρ������κ͵������ζ���������ı��Σ���Ҷ������ǵ����ʶ��dz���Ϥ�������л���һ��������ı��Ω������Σ���ν���Σ�������״�����������з��ݵĹǼ����ƣ� |
|
���ֻ�о�һ������Σ����������Σ�����������ϲ��������������
���ֻ�о�һ������Σ����������Σ�����������ϲ��������������
��1����˵�����κ����ε���ͬ��Ͳ�ͬ���������
��2�������ͼ1�Ļ�������ͼ2��ʾ��8��8�������������һ�����ĸ�ȫ�ȵ����κ��ĸ�ȫ�ȵ�������ɵ���ͼ��������Ҫ�����£�
�ٶ��㶼�ڸ���ϣ�
������Ƶ�ͼ��������Գ�ͼ���������ĶԳ�ͼ�Σ�
�۽���ͼ���е��ĸ����ζ�ͼ����Ӱ��������һϵ��ƽ��б�߱�ʾ��Ӱ����






