题目内容
【题目】在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2﹣1.
(1)求抛物线顶点C的坐标(用含m的代数式表示);
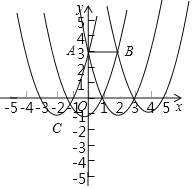
(2)已知点A(0,3),B(2,3),若该抛物线与线段AB有公共点,结合函数图象,求出m的取值范围.
【答案】(1)C(m,﹣1);(2)﹣2≤m≤0或2≤m≤4.
【解析】
(1)化成顶点式,即可求得顶点C的坐标;
(2)由顶点C的坐标可知,抛物线的顶点C在直线y=﹣1上移动.分别求出抛物线过点A、点B时,m的值,画出此时函数的图象,结合图象即可求出m的取值范围.
(1)y=x2﹣2mx+m2﹣1=(x﹣m)2﹣1,
∴抛物线顶点为C(m,﹣1).
(2)把A(0,3)的坐标代入y=x2﹣2mx+m2﹣1,
得3=m2﹣1,
解得 m=±2.
把B(2,3)的坐标代入y=x2﹣2mx+m2﹣1,
得3=22﹣2m×2+m2﹣1,
即m2﹣4m=0,
解得m=0 或m=4.
结合函数图象可知:﹣2≤m≤0或2≤m≤4.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
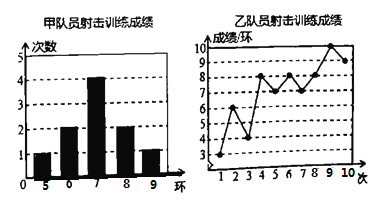
根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)写出表格中![]() 的值:
的值:
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?