Question

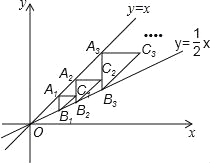
【题目】如图，点A1（2，2）在直线y=x上，过点A1作A1B1∥y轴交直线y=x于点B1，以点A1为直角顶点，A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1，再过点C1作A2B2∥y轴，分别交直线y=x和y=x于A2，B2两点，以点A2为直角顶点，A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…，按此规律进行下去，则等腰直角△AnBnCn的面积为 ．（用含正整数n的代数式表示）

Answer 1

【答案】．

【解析】

试题分析：∵点A1（2，2），A1B1∥y轴交直线y=x于点B1，

∴B1（2，1）

∴A1B1=2﹣1=1，即△A1B1C1面积=×12=；

∵A1C1=A1B1=1，

∴A2（3，3），

又∵A2B2∥y轴，交直线y=x于点B2，

∴B2（3，），

∴A2B2=3﹣=，即△A2B2C2面积=×（）2=；

以此类推，

A3B3=，即△A3B3C3面积=×（）2=；

A4B4=，即△A4B4C4面积=×（）2=；

…

∴AnBn=（）n﹣1，即△AnBnCn的面积=×[（）n﹣1]2=．