题目内容
【题目】在平面直角坐标系上,已知点 A(8,4),AB⊥y轴于 B,AC⊥x轴于 C,直线 y=x交 AB于 D.
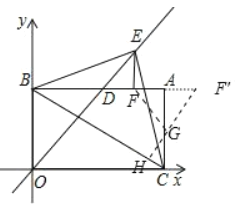
(1)如图 1,若 E 为 OD 延长线上一动点,当△BCE 的面积,S△BCE=20 时,过点 E 作 EF⊥AB于 F,点 G、H 分别为 AC、CB 上动点,求 FG+GH 的最小值及点 G 的坐标.
(2)如图 2,直线 BC 与 DE 交于点 M,作直线 MN∥y 轴,在(1)的条件下,将△DEF 沿 DE方向平移![]() 个单位得到△D′E′F′,在直线 MN 上是否存在点 P 使得△BF′P 为等腰三角形,若存在请直接写出满足条件的点 P 的坐标;若不存在,请说明理由.
个单位得到△D′E′F′,在直线 MN 上是否存在点 P 使得△BF′P 为等腰三角形,若存在请直接写出满足条件的点 P 的坐标;若不存在,请说明理由. 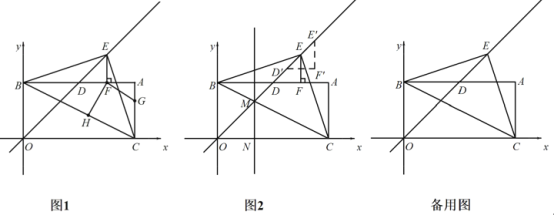
【答案】(1)![]() 的最小值为
的最小值为![]() ,G(8,0);
,G(8,0);
(2)存在,满足条件的P点有五个,坐标为: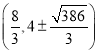 或
或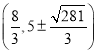 或
或![]() ,理由见解析.
,理由见解析.
【解析】
(1)先分别求得A、B、C三点坐标,根据直线y=x交AB于D,可求D点坐标,设![]() ,根据S△BCE=20可求得E点坐标,由此可求得F点坐标,作点F关于直线AC的对称点F',作F'H⊥BC于H,可得F'H即为FG+GH 的最小值,证明
,根据S△BCE=20可求得E点坐标,由此可求得F点坐标,作点F关于直线AC的对称点F',作F'H⊥BC于H,可得F'H即为FG+GH 的最小值,证明![]() ,借助相似的性质可求F'H的长度,借助勾股定理求得
,借助相似的性质可求F'H的长度,借助勾股定理求得![]() ,由此得出G点与C点重合,即可得出G点坐标;
,由此得出G点与C点重合,即可得出G点坐标;
(2)求出平移后F'坐标,证明△BMD∽△CMO,由此可求得M点坐标,即可得出P点横坐标,设![]() ,利用距离公式分别表示
,利用距离公式分别表示![]() ,利用它们两两相等分三种情况讨论即可.
,利用它们两两相等分三种情况讨论即可.
(1)∵AB⊥y轴于B,AC⊥x轴于C,
∴∠ABO=∠ACO=∠COB=90°,
∴四边形ABOC是矩形,
∵A(8,4),
∴AB=OC=8,AC=OB=4,
∴B(0,4),C(8,0),
∵直线y=x交AB于D,
∴∠BOD=45°,
∴OB=DB=4,
∴D(4,4).
设![]()
![]()
当S=20时,20=6a16,
解得a=6,
∴E(6,6),
∵EF⊥AB于F,
∴F(6,4),
如下图,作点F关于直线AC的对称点F',作F'H⊥BC于H,交AC于G.此时FG+GH的值最小.
![]()
![]()
![]()
![]()
![]()
![]()
在![]() 中,根据勾股定理
中,根据勾股定理
![]()
因此H、C、G三点重合,G(8,0)
![]() 的最小值为
的最小值为![]() ,G(8,0);
,G(8,0);
(2)如下图:作![]() 于K,由题意得
于K,由题意得![]()
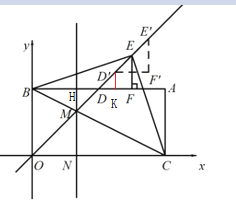
∵四边形ABOC为矩形
∴AB//OC
∴∠EDA=∠EOA=45°
∴![]() 为等腰直角三角形,
为等腰直角三角形,
![]()
又![]()
∴![]()
∴△DEF向右平移一个单位,向上平移一个单位得到△D′E′F′
∵F(6,4)
∴F′(7,5)
∵AB//OC
∴△BMD∽△CMO
∴![]()
又∵HM+MN=OB=4
∴MN=![]() ,即
,即![]()
设P点坐标为![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
①若![]() ,则
,则![]() 即
即
![]()
解得![]() ,
,
②若![]() 则
则![]() 即
即
![]()
解得![]()
③若![]() 则
则![]() 即
即
![]()
解得![]()
综上满足条件的P点有五个,坐标为: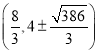 或
或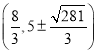 或
或![]() .
.