题目内容
【题目】已知:如图,点D是△ABC中BC边上的中点,DE⊥AC,DF⊥AB,垂足分别是点EF,且BF=CE.
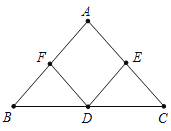
(1)求证:Rt△BDF≌Rt△CDE
(2)问:△ABC满足什么条件时,四边形AEDF是正方形,并说明理由.
【答案】(1)见解析;(2)当△ABC满足∠A=90°(答案不唯一)时,四边形AEDF是正方形,理由见解析
【解析】
(1)先利用HL判定Rt△BDF≌Rt△CDE即可;
(2)由已知可证明四边形AEDF是矩形,由全等三角形的性质得出DE=DF,即可得出结论.
∵DE⊥AC,DF⊥AB,
∴∠BDF=∠CED=90°
∵点D是△ABC中BC边上的中点,
∴BD=CD,在Rt△BDF和Rt△CDF中,![]() ,
,
∴Rt△BDF≌Rt△CDE(HL);
(2)解:当△ABC满足∠A=90°(答案不唯一)时,四边形AEDF是正方形;理由如下:
∵∠BDF=∠CED=90°,∠A=90°,
∴四边形AEDF是矩形,
∵Rt△BDF≌Rt△CDE,
∴DE=DF,
∴四边形AEDF是正方形.

练习册系列答案
相关题目