题目内容
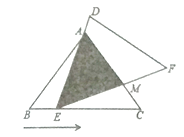
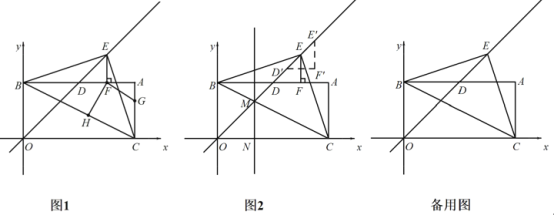
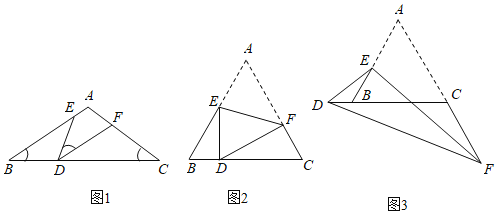
【题目】(1)模型探究:如图1,D、E、F分别为△ABC三边BC、AB、AC上的点,且∠B=∠C=∠EDF=a.△BDE与△CFD相似吗?请说明理由;
(2)模型应用:△ABC为等边三角形,其边长为8,E为AB边上一点,F为射线AC上一点,将△AEF沿EF翻折,使A点落在射线CB上的点D处,且BD=2.
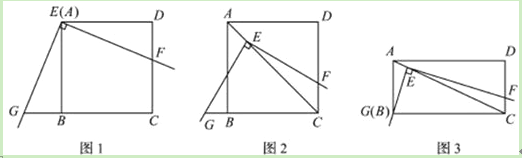
①如图2,当点D在线段BC上时,求![]() 的值;
的值;
②如图3,当点D落在线段CB的延长线上时,求△BDE与△CFD的周长之比.
【答案】(1)△BDE∽△CFD,理由见解析;(2)①![]() ;②
;②![]()
【解析】
(1)利用等式的性质判断出∠BED=∠CDF,即可得出结论;
(2)①同(1)的方法判断出△BDE∽△CFD,得出比例式,再设出AE=x,AF=y,进而表示出BE=8-x,CF=8-y,CD=6,代入比例式化简即可得出结论;
②同①的方法即可得出结论.
(1)△BDE∽△CFD,
理由:∠B=∠C=∠EDF=a,
在△BDE中,∠B+∠BDE+∠BED=180°,
∴∠BDE+∠BED=180°-∠B=180°-α,
∵∠BDE+∠EDF+∠CDF=180°,
∴∠BDE+∠CDF=180°-∠EDF=180°-α,
∴∠BED=∠CDF,
∵∠B=∠C,
∴△BDE∽△CFD;
(2)①设AE=x,AF=y,
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC=8,
由折叠知,DE=AE=x,DF=AF=y,∠EDF=∠A=60°,
在△BDE中,∠B+∠BDE+∠BED=180°,
∴∠BDE+∠BED=180°-∠B=120°,
∵∠BDE+∠EDF+∠CDF=180°,
∴∠BDE+∠CDF=180°-∠EDF=120°,
∴∠BED=∠CDF,
∵∠B=∠C=60°,
∴△BDE∽△CFD,
∴![]()
∵BE=AB-AE=8-x,CF=AC-AF=8-y,CD=BC-BD=6,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
②设AE=x,AF=y,
∵△ABC是等边三角形,
∴∠A=∠ABC=∠ACB=60°,AB=BC=AC=8,
由折叠知,DE=AE=x,DF=AF=y,∠EDF=∠A=60°,
在△BDE中,∠ABC+∠BDE+∠BED=180°,
∴∠BDE+∠BED=180°-∠ABC=120°,
∵∠BDE+∠EDF+∠CDF=180°,
∴∠BDE+∠CDF=180°-∠EDF=120°,
∴∠BED=∠CDF,
∵∠ABC=∠ACB=60°,
∴∠DBE=∠DCF=120°,
∴△BDE∽△CFD,
∴![]()
∵BE=AB-AE=8-x,CF=AF-AC=y-8,CD=BC+BD=10,
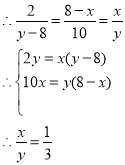 .
.
∵△BDE∽△CFD,
∴△BDE与△CFD的周长之比为![]() .
.