题目内容
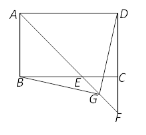
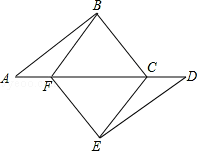
【题目】如图,点A.F、C.D在同一直线上,点B和点E分别在直线AD的两侧,且
AB=DE,∠A=∠D,AF=DC.
(1)求证:四边形BCEF是平行四边形,
(2)若∠ABC=90°,AB=4,BC=3,当AF为何值时,四边形BCEF是菱形.
【答案】(1)证明:∵AF=DC,∴AF+FC=DC+FC,即AC=DF。
∵在△ABC和△DEF中,AC=DF,∠A=∠D,AB=DE,
∴△ABC≌DEF(SAS)。∴BC=EF,∠ACB=∠DFE,∴BC∥EF。
∴四边形BCEF是平行四边形.
(2)解:连接BE,交CF与点G,
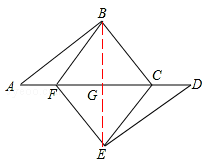
∵四边形BCEF是平行四边形,
∴当BE⊥CF时,四边形BCEF是菱形。
∵∠ABC=90°,AB=4,BC=3,
∴AC=![]() 。
。
∵∠BGC=∠ABC=90°,∠ACB=∠BCG,∴△ABC∽△BGC。
∴![]() ,即
,即![]() 。∴
。∴![]() 。
。
∵FG=CG,∴FC=2CG=![]() ,
,
∴AF=AC﹣FC=5﹣![]() 。
。
∴当AF=![]() 时,四边形BCEF是菱形.
时,四边形BCEF是菱形.
【解析】(1)由AB=DE,∠A=∠D,AF=DC,根据SAS得△ABC≌DEF,即可得BC=EF,且BC∥EF,即可判定四边形BCEF是平行四边形。
(2)由四边形BCEF是平行四边形,可得当BE⊥CF时,四边形BCEF是菱形,所以连接BE,交CF与点G,证得△ABC∽△BGC,由相似三角形的对应边成比例,即可求得AF的值。

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目