Question

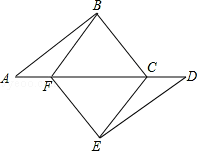
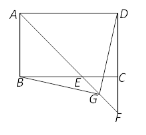
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F.

（1）若AB=2,AD=3,求EF的长；

（2）若G是EF的中点,连接BG和DG,求证：DG=BG.

Answer 1

【答案】（1）EF＝；（2）见解析

【解析】

（1）由AE平分∠BAD，可得∠DAF＝45°，从而∠F＝45°，可证△ADF，△ECF都是等腰直角三角形，求出CF的长，最后根据勾股定理即可求出EF的长；

（2）连结CG，易证∠BEG＝∠DCG＝135°，根据“SAS”可证△BEG≌△DCG，从而可得DG＝BG.

解：（1）在矩形ABCD中

∵AE平分∠BAD,

∴∠DAF＝45°,

∴∠F＝45°，

∴△ADF，△ECF都是等腰直角三角形，

∴DF＝AD＝3, CF＝DF－CD= 1.

在Rt△CEF中,

∴EF＝.

（2）连结CG,

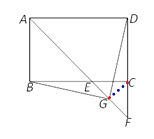
∵G是EF中点,

∴CG⊥EF,

∠ECG＝∠CEF＝45°.

∴∠BEG＝∠DCG＝135°.

∴EG＝EF＝CG.

∵AB＝BE＝CD,

∴BE＝CD.

∴△BEG≌△DCG,

∴DG＝BG.