题目内容
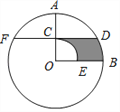
【题目】如图,AB为直径,AB=4,C、D为圆上两个动点,N为CD中点,CM⊥AB于M,当C、D在圆上运动时保持∠CMN=30°,则CD的长( )
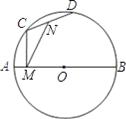
A. 随C、D的运动位置而变化,且最大值为4 B. 随C、D的运动位置而变化,且最小值为2
C. 随C、D的运动位置长度保持不变,等于2 D. 随C、D的运动位置而变化,没有最值
【答案】C
【解析】分析:连接OC、ON、OD,由垂径定理可知ON⊥CD,∠CON=∠DON,然后由∠ONC+∠CMO=180°,可证明O、N、C、M四点共圆,从而可得到∠NOC=∠NMC=30°,于是可证明△OCD为等边三角形,从而得到CD=2.
详解:连接:OC、ON、OD.
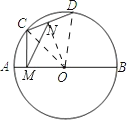
∵N是CD的中点,
∴ON⊥CD,∠CON=∠DON.
又∵CM⊥AB,
∴∠ONC+∠CMO=180°,
∴O、N、C. M四点共圆,
∴∠NOC=∠NMC=30°,
∴∠COD=60°,
又∵OC=OD,
∴△OCD为等边三角形.
∴CD=![]() AB=
AB=![]() ×4=2.
×4=2.
故选:C.

练习册系列答案
相关题目