题目内容
【题目】已知点![]() 和直线
和直线![]() (
(![]() 不同时为0),则点
不同时为0),则点![]() 到直线
到直线![]() 的距离
的距离![]() 可用公式
可用公式![]() 计算.
计算.
例如.求点![]() 到直线
到直线![]() 的距离.
的距离.
解:由直线可知![]()
∴![]()
根据以上材料,解答下列问题:
(1) 求点![]() 到直线
到直线![]() 的距离;
的距离;
(2) 求点![]() 到直线
到直线![]() 的距离,并说明点
的距离,并说明点![]() 与直线的位置关系;
与直线的位置关系;
(3)已知直线![]() 与直线
与直线![]() 平行,求两条平行线间的距离.
平行,求两条平行线间的距离.
【答案】(1)![]() ;(2)0,
;(2)0,![]() 在直线
在直线![]() 上;(3)
上;(3)![]()
【解析】
(1)由点![]() 到直线的距离公式计算即可;
到直线的距离公式计算即可;
(2)先把直线解析式整理成一般式,再由点![]() 到直线的距离公式计算即可;
到直线的距离公式计算即可;
(3)平行线间的距离是其中一条平行直线上某一点到另一条平行线的距离.
(1)由直线![]() 可知
可知![]() ,
,
则点![]() 到直线
到直线![]() 的距离
的距离 ;
;
(2)直线![]() 变形为
变形为![]() ,
,
则![]() ,
,
则点![]() 到直线
到直线![]() 的距离
的距离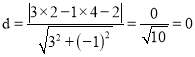 ,
,
故点![]() 在直线
在直线![]() 上;
上;
(3)在直线![]() 取一点P,
取一点P,
当y=0时,x=-1,
故![]() ,
,
则![]() 到直线
到直线![]() 的距离就是两平行线间的距离:
的距离就是两平行线间的距离: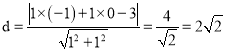 .
.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
【题目】为鼓励居民节约用电,某市采用价格调控手段达到省电目的,该市电费收费标准如下表(按月结算):
每月用电量度 | 电价/(元/度) |
不超过150度的部分 | 0.50元/度 |
超过150度且不超过250度的部分 | 0.65元/度 |
超过250度的部分 | 0.80元/度 |
问:(1)某居民12月份用电量为180度,请问该居民12月应缴交电费多少元?
(2)设某月的用电量为![]() 度(
度(![]() ),试写出不同电量区间应缴交的电费.
),试写出不同电量区间应缴交的电费.