题目内容
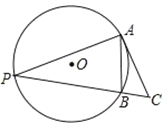
【题目】如图,四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() ,连接
,连接![]() .
.
求证:(1)![]() ;(2)
;(2)![]() .
.
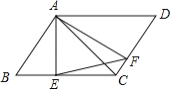
【答案】(1)见解析;(2)见解析
【解析】
(1)根据平行四边形的性质得出∠B=∠D,再利用∠AEB=∠AFD=90°,得出△ABE∽△ADF,进而得出ABAF=AEAD;
(2)根据平行四边形的性质得出AB∥CD,进而得出∠B=∠EAF,即可得出![]() ,即可得出△ABC∽△EAF,即可得出答案.
,即可得出△ABC∽△EAF,即可得出答案.
证明:(1)∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
∴△ABE∽△ADF,
∴![]() ,
,
即ABAF=AEAD;
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAF=∠AFD=90°,
∵∠B+∠BAE=90°,∠EAF+∠BAE=90°,
∴∠B=∠EAF,
∵△ABE∽△ADF,
∴![]() ,
,
又∵AD=BC,
∴![]() ,
,
∴△ABC∽△EAF,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目