题目内容
如图,四边形ABCD为矩形,点C与点D在x轴上,且点A的坐标为(1,3).已知直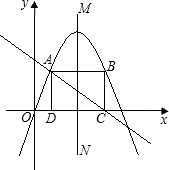 线y=-
线y=-| 3 |
| 4 |
| 15 |
| 4 |
(1)求出C点的坐标;
(2)求抛物线的解析式;
(3)若直线MN为抛物线的对称轴,E为x轴上的一个动点,则是否存在以E点为圆心,且同时与直线MN和直线AC都相切的圆?如果存在,请求出⊙E的半径;如果不存在,请说明理由.
分析:(1)本题需先根据点C在x轴上,得出y=0,再把它代入直线,得出x的值,即可求出C点的坐标.
(2)本题根据C点的坐标和A的坐标,得出B点的坐标,再根据抛物线y=ax2+bx经过A、B两点,求出a、b的值,即可求出解析式.
(3)本题需先判断出存在,再结合图形分两种情况进行讨论,当⊙E与直线MN和直线AC都相切时,设半径为R,再过点E作EF⊥AC,得出EH、EF的长,再由勾股定理得出AC的值,再由已知条件得出△ECF与△GCH相似,即可求出⊙E的半径;再结合图形当在对称轴MN的右侧,同理也可求出R的值.
(2)本题根据C点的坐标和A的坐标,得出B点的坐标,再根据抛物线y=ax2+bx经过A、B两点,求出a、b的值,即可求出解析式.
(3)本题需先判断出存在,再结合图形分两种情况进行讨论,当⊙E与直线MN和直线AC都相切时,设半径为R,再过点E作EF⊥AC,得出EH、EF的长,再由勾股定理得出AC的值,再由已知条件得出△ECF与△GCH相似,即可求出⊙E的半径;再结合图形当在对称轴MN的右侧,同理也可求出R的值.
解答:解:(1)∵点C在x轴上,
∴把y=0代入y=-
x+
,
解得:x=5.
∴C点的坐标为(5,0);
(2)∵C点的坐标为(5,0),A的坐标为(1,3),四边形ABCD为矩形,
∴B点的坐标为(5,3),
∵抛物线y=ax2+bx经过A、B两点.
∴
,
解得:a=-
;b=
.
∴y=-
x2+
x;
(3)存在.
①如图,⊙E与直线MN和直线AC都相切,设半径为R,过点E作EF⊥AC,垂足为F.则EH=EF=R.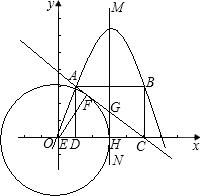
在Rt△ADC中,由勾股定理得,AC=
=
=5.
依题意得:CH=DH,GH∥AD,
∴GH=
AD=
;CG=
AC=
.
∵∠CFE=∠CHG=90°,∠ECF=∠GCH,
∴△ECF∽△GCH,
∴
=
即
=
,
解得:R=3;
②在对称轴MN的右侧,同理可求得:R=
.
综上,符合条件的圆心E有两点,所对应的半径分别是3和
.
∴把y=0代入y=-
| 3 |
| 4 |
| 15 |
| 4 |
解得:x=5.
∴C点的坐标为(5,0);
(2)∵C点的坐标为(5,0),A的坐标为(1,3),四边形ABCD为矩形,
∴B点的坐标为(5,3),
∵抛物线y=ax2+bx经过A、B两点.
∴
|
解得:a=-
| 3 |
| 5 |
| 18 |
| 5 |
∴y=-
| 3 |
| 5 |
| 18 |
| 5 |
(3)存在.
①如图,⊙E与直线MN和直线AC都相切,设半径为R,过点E作EF⊥AC,垂足为F.则EH=EF=R.

在Rt△ADC中,由勾股定理得,AC=
| AD2+CD2 |
| 32+42 |
依题意得:CH=DH,GH∥AD,
∴GH=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∵∠CFE=∠CHG=90°,∠ECF=∠GCH,
∴△ECF∽△GCH,
∴
| EF |
| GH |
| CE |
| CG |
| R |
| 1.5 |
| R+2 |
| 2.5 |
解得:R=3;
②在对称轴MN的右侧,同理可求得:R=
| 3 |
| 4 |
综上,符合条件的圆心E有两点,所对应的半径分别是3和
| 3 |
| 4 |
点评:本题主要考查了二次函数的综合,在解题时要结合图形以及二次函数的各个知识点,将它们综合起来解此题是本题的关键.

练习册系列答案
相关题目
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条) 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF. 如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数. 如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.
如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.