Question

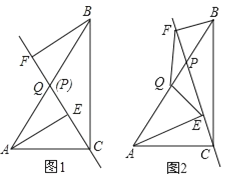
【题目】如图,已知△ABC和△BDE都是等边三角形。则下列结论：①AE=CD.②BF=BG.③HB⊥FG.④∠AHC=60.⑤△BFG是等边三角形，其中正确的有___.

Answer 1

【答案】①②④⑤

【解析】

由题中条件可得△ABE≌△CBD，得出对应边、对应角相等，进而得出△BGD≌△BFE，△ABF≌△CGB，再由边角关系即可求解题中结论是否正确，进而可得出结论．

∵△ABC与△BDE为等边三角形,

∴AB=BC,BD=BE,∠ABC=∠DBE=60，

∴∠ABE=∠CBD，

即AB=BC，BD=BE，∠ABE=∠CBD，故①正确

∴△ABE≌△CBD，

∴AE=CD，∠BDC=∠AEB，

又∵∠DBG=∠FBE=60，

∴△BGD≌△BFE，

∴BG=BF,∠BFG=∠BGF=60，故②正确，

∴△BFG是等边三角形，故⑤正确，

∴FG∥AD，

∵BF=BG,AB=BC,∠ABF=∠CBG=60，

∴△ABF≌△CGB，

∴∠BAF=∠BCG，

∴∠CAF+∠ACB+∠BCD=∠CAF+∠ACB+∠BAF=60°+60°=120°，

∴∠AHC=60°，故④正确，

∵∠FGB=∠GBD=60°，

∴FG∥AD，

不妨设FG⊥BH,则BH⊥AD,易证△ABH≌△DBH，可得AB=BD，显然与已知条件矛盾，故③错误，

故答案为①②④⑤.