题目内容
【题目】在2016年巴西里约奥运会上，中国女排克服重重困难，凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队，荷兰队和塞尔维亚队，获得了奥运冠军，为祖国和人民争了光．
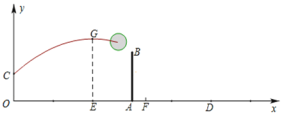
如图，已知女排球场的长度OD为18米，位于球场中线处的球网AB的高度为2.24米，一队员站在点O处发球，排球从点O的正上方2米的C点向正前方飞去，排球的飞行路线是抛物线的一部分，当排球运行至离点O的水平距离OE为6米时，到达最高点F，以O为原点建立如图所示的平面直角坐标系．
（1）当排球运行的最大高度为2.8米时，求排球飞行的高度y（单位：米）与水平距离x（单位：米）之间的函数关系式．
（2）在（1）的条件下，这次所发的球能够过网吗？如果能够过网，是否会出界？请说明理由．
（3）喜欢打排球的李明同学经研究后发现，发球要想过网，球运行的最大高度h（米）应满足h＞2.32，但是他不知道如何确定h的取值范围，使排球不会出界（排球压线属于没出界），请你帮忙解决并指出使球既能过网又不会出界的h的取值范围 .
【答案】(1) y=
(x6)+2.8；(2)这次发球可以过网且不出边界；(3)h
.
【解析】
（1）根据此时抛物线顶点坐标为（6，2.8），设解析式为y=a（x-7)2+3.2，再将点C坐标代入即可求得；（2）把x=9，x=18代入（1）中的解析式，与2.24和0比较即可.（3）设抛物线解析式为y=a（x-6）2+h，将点C坐标代入得到用h表示a的式子，再根据球既要过球网，又不出边界即x=9时，y＞2.24且x=18时，y≤0得出关于h的不等式组，解之即可得．
(1)由题意可得抛物线的顶点F的坐标为(6,2.8)，
设抛物线的解析式为y=a(x6)+2.8，
将点C(0,2)代入，得：36a+2.8=2，
解得：a=，
∴y= (x6)+2.8；
(2)当x=9时,y= (96)+2.8=2.6>2.24，
当x=18时,y=(186)+2.8=0.4<0，
∴这次发球可以过网且不出边界；
(3)设抛物线解析式为y=a(x6)+h，
将点C(0,2)代入,得：36a+h=2,即a=
，
∴此时抛物线解析式为y=(x6)+h，
根据题意,得：
+h0，
解得：h，
又∵h>2.32，
∴h
答：球既能过网又不会出界的h的取值范围是h.
