题目内容
【题目】如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为1个单位,运动时间为t秒.过点P作PE⊥AO交AB于点E.
(1)求直线AB的解析式;
(2)设△PEQ的面积为S,求S与t时间的函数关系,并指出自变量t的取值范围;
(3)在动点P、Q运动的过程中,点H是矩形AOBC内(包括边界)一点,且以B、Q、E、H为顶点的四边形是菱形,直接写出t值和与其对应的点H的坐标.

【答案】(1)直线AB的解析式为y=﹣2x+4.(2)S![]() t2﹣t(2<t≤4).(3)t1=
t2﹣t(2<t≤4).(3)t1=![]() ,H1(
,H1(![]() ),t2=20﹣
),t2=20﹣![]() ,H2(10﹣
,H2(10﹣![]() ,4).
,4).
【解析】试题分析:(1)根据待定系数法即可得到;
(2)过点Q作QF//x轴交y轴于点F,有两种情况:当0<t<2时,PF=4﹣2t,当2<t≤4时,PF=2t﹣4,然后根据面积公式即可求得;
(3)由菱形的邻边相等即可得到.
试题解析:(1)∵C(2,4),
∴A(0,4),B(2,0),
设直线AB的解析式为y=kx+b,
∴![]() ,
,
解得![]()
∴直线AB的解析式为y=﹣2x+4.
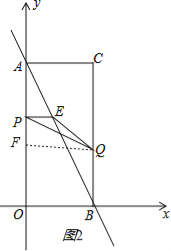
(2)如图2,过点Q作QF⊥y轴于F,
∵PE//OB,
∴![]()
∴有AP=BQ=t,PE=![]() t,AF=CQ=4﹣t,
t,AF=CQ=4﹣t,
当0<t<2时,PF=4﹣2t,
∴S=![]() PEPF=
PEPF=![]() ×
×![]() t(4﹣2t)=t﹣
t(4﹣2t)=t﹣![]() t2,
t2,
即S=﹣![]() t2+t(0<t<2),
t2+t(0<t<2),
当2<t≤4时,PF=2t﹣4,
∴S=![]() PEPF=
PEPF=![]() ×
×![]() t(2t﹣4)=
t(2t﹣4)=![]() t2﹣t(2<t≤4).
t2﹣t(2<t≤4).
(3)t1=![]() ,H1(
,H1(![]() ,
,![]() ),
),
t2=20﹣8![]() ,H2(10﹣4
,H2(10﹣4![]() ,4).
,4).

练习册系列答案
相关题目