题目内容
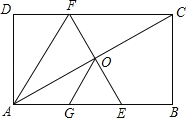
【题目】如图,在矩形ABCD中,O为AC中点,EF过点O且EF⊥AC分别交DC于点F,交AB于点E,点G是AE中点且∠AOG=30°,给出以下结论:
①∠AFC=120°;
②△AEF是等边三角形;
③AC=3OG;
④S△AOG=![]() S△ABC
S△ABC
其中正确的是______.(把所有正确结论的序号都选上)
【答案】①②④.
【解析】试题分析:根据直角三角形斜边上的中线等于斜边的一半可得OG=AG=GE=![]() AE,再根据等边对等角可得∠OAG=30°,∠EOG=60°,从而根据矩形的性质得到∠ACF=30°,因此由线段垂直平分线的性质可得FC=AF,因此可根据等边对等角得到∠FAE=30°,根据三角形的内角和求得∠AFC=120°,故①正确;
AE,再根据等边对等角可得∠OAG=30°,∠EOG=60°,从而根据矩形的性质得到∠ACF=30°,因此由线段垂直平分线的性质可得FC=AF,因此可根据等边对等角得到∠FAE=30°,根据三角形的内角和求得∠AFC=120°,故①正确;
由∠AFC=120°,∠FCA=30°,可知∠AFE=60°,因此△AEF是等边三角形,故②正确;
连接CE,则根据三角形的中位线可知CE=2OG,由矩形的性质可得四边形AECF是菱形,且![]() ,由OE=OG,OA=
,由OE=OG,OA=![]() AC,可知
AC,可知![]() ,解得AC=
,解得AC=![]() OG,故③不正确;
OG,故③不正确;
令AE=2a,则OG=OE=a,AO=![]() a,AC=2
a,AC=2![]() a,由S△AOE=
a,由S△AOE=![]() ×a×
×a×![]() a=
a=![]() 2,S矩形ABCD=3a×
2,S矩形ABCD=3a×![]() a=3
a=3![]() a2 ,即S△AOG=
a2 ,即S△AOG=![]() S△ABC,故④正确.
S△ABC,故④正确.
故答案为:①②④.

练习册系列答案
相关题目
【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:
次数 | 60≤x<90 | 90≤x<120 | 120≤x<150 | 150≤x<180 | 180≤x<210 |
频数 | 16 | 25 | 9 | 7 | 3 |
(1)全班有多少同学?
(2)组距是多少?组数是多少?
(3)跳绳次数x在120≤x<180范围的同学有多少?占全班同学的百分之几?
(4)画出适当的统计图表示上面的信息.