题目内容
【题目】如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上,如果用(1,0)表示C点的位置,用(4,1)表示B点的位置,那么.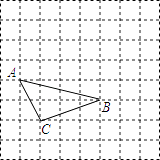
(1)画出直角坐标系;
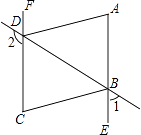
(2)画出与△ABC关于x轴对称的图形△DEF;
(3)P为x轴上的一个动点,是否存在P使PA+PB的值最小?若不存在,请说明理由;若存在请求出点P的坐标和PA+PB的最小值.
【答案】
(1)
解:如图所示:
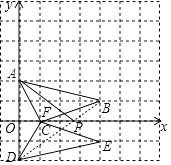
(2)
解:如图所示:

(3)
解:存在,连接BD交x轴于点P,连接PA,由对称可知D(0,﹣2),
设直线BD的表达式为y=kx+b,则有B=﹣2,4k+b=1,
解得:k= ![]() ,b=﹣2,
,b=﹣2,
所以直线BD的表达式为y= ![]() x﹣2,
x﹣2,
当y=0时,有 ![]() x﹣2=0,
x﹣2=0,
解得x= ![]() ,
,
所以P( ![]() ,0),
,0),
由对称可知PA=PD,所以PA+PB=PD+PB=DB= ![]() =5.
=5.
【解析】(1)根据C点坐标可确定原点位置,然后可画出坐标系;(2)首先确定A、B、C三点关于x轴对称的对称点位置,然后连接即可;(3)连接BD交x轴于点P,连接PA,设直线BD的表达式为y=kx+b,利用待定系数法确定解析式,然后根据解析式确定P点坐标,再利用勾股定理计算出BD的长.
【考点精析】本题主要考查了作轴对称图形的相关知识点,需要掌握画对称轴图形的方法:①标出关键点②数方格,标出对称点③依次连线才能正确解答此题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目