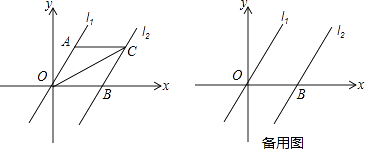题目内容
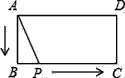
【题目】如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2），动点M在y轴上运动．
（1）求直线AB的函数解析式；
（2）动点M在y轴上运动，使MA+MB的值最小，求点M的坐标；
（3）在y轴的负半轴上是否存在点M，使△ABM是以AB为直角边的直角三角形？如果存在，求出点M的坐标；如果不存在，说明理由．
【答案】（1）y=-x+6；（2）M（0，
）；（3）（0，-2）或（0，-6）.
【解析】
（1）设AB的函数解析式为：y=kx+b，把A、B两点的坐标代入解方程组即可.
（2）作点B关于y轴的对称点B′，则B′点的坐标为（-6，0），连接AB′则AB′为MA+MB的最小值，根据A、B′两点坐标可知直线AB′的解析式，即可求出M点坐标，（3）分别考虑∠MAB为直角时直线MA的解析式，∠ABM′为直角时直线BM′的解析式，求出M点坐标即可，
（1）设直线AB的函数解析式为y=kx+b,则
解方程组得
直线AB的函数解析式为y= -x+6，
（2）如图作点B关于y轴的对称点B′，则点B′的坐标为（-6，0），连接AB′则AB′为MA+MB的最小值，设直线AB′的解析式为y=mx+n，则
，
解方程组得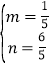
所以直线AB′的解析式为
，
当x=0时，y=，
所以M点的坐标为（0，），
（3）有符合条件的点M，理由如下：
如图：因为△ABM是以AB为直角边的直角三角形，
当∠MAB=90°时，直线MA垂直直线AB，
∵直线AB的解析式为y=-x+6，
∴设MA的解析式为y=x+b，
∵点A（4，2），
∴2=4+b,
∴b=-2，
当∠ABM′=90°时，BM′垂直AB，
设BM′的解析式为y=x+n,
∵点B（6，0）
∴6+n=0
∴n=-6,
即有满足条件的点M为（0，-2）或（0，-6）.
