Question

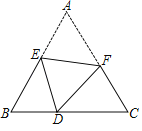
【题目】如图，将等边三角形ABC折叠，使得点A落在BC边上的点D处，折痕为EF，点E，F分别在AB和AC边上．若AB＝6，BD＝2，则AE：AF的值为_____．

Answer 1

【答案】

【解析】

由已知求得CD＝3a，根据等边三角形的性质和折叠的性质可得：BE+DE+BD＝8，DF+CF+CD＝10，再证明△BED∽△CDF，由相似三角形周长的比等于相似比，即可得出结果．

∵△ABC是等边三角形，

∴BC＝AB＝AC＝6，∠ABC＝∠ACB＝∠BAC＝60°，

∵BD＝2，

∴CD＝4，

由折叠的性质可知：AE＝DE，AF＝DF，∠EDF＝∠A＝60°，

∴BE+DE+BD＝AB+BD＝8，DF+CF+CD＝AC+CD＝10，

∵∠EDF＝∠BAC＝∠ABC＝60°，

∴∠FDC+∠EDB＝∠BED+∠EBD＝120°，

∴∠FDC＝∠BED，

∵∠B＝∠C＝60°，

∴△BED∽△CDF，

∴（BE+DE+BD）：（DF+CF+CD）＝DE：DF＝AE：AF，

∴

故答案为： ．