题目内容
【题目】定义:点P(a,b)关于原点的对称点为P′,以PP′为边作等边△PP′C,则称点C为P的“等边对称点”;
(1)若P(1,3),求点P的“等边对称点”的坐标.
(2)平面内有一点P(1,2),若它其中的一个“等边对称点”C在第四象限时,请求此C点的坐标;
(3)若P点是双曲线y=![]() (x>0)上一动点,当点P的“等边对称点”点C在第四象限时,
(x>0)上一动点,当点P的“等边对称点”点C在第四象限时,
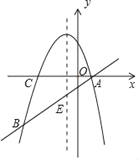
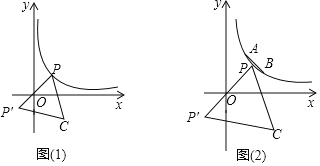
①如图(1),请问点C是否也会在某一函数图象上运动?如果是,请求出此函数的解析式;如果不是,请说明理由.
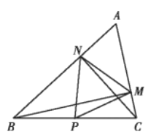
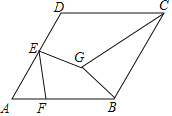
②如图(2),已知点A (1,2),B (2,1),点G是线段AB上的动点,点F在y轴上,若以A、G、F、C这四个点为顶点的四边形是平行四边形时,求点C的纵坐标yc的取值范围.
【答案】(1)C ![]() 或C(
或C(![]() ;(3)yc≤﹣6或﹣3<yc≤﹣2;
;(3)yc≤﹣6或﹣3<yc≤﹣2;
【解析】
(1)由定义可知P’的坐标,设C坐标为(m,n),进而根据两点坐标公式和等边三角形三边相等即可列出方程求解即可.
(2)同(1)求出点C坐标,根据它其中的一个“等边对称点”C在第四象限可得C点坐标.
(3)①设P(c,![]() ),则P'(﹣c,﹣
),则P'(﹣c,﹣![]() ),设C点坐标为(s,t),同(1)列方程组即可求出C点坐标为
),设C点坐标为(s,t),同(1)列方程组即可求出C点坐标为![]() ,即可求出点C运动的函数解析式.
,即可求出点C运动的函数解析式.
②设G点横坐标为t,则由直线AB解析式可知G点坐标为(t,-t+3),由F点在x轴可知其横坐标为0,分两种情况可:I. 当AG为平行四边形的边时,则C点坐标为(t-1,yc),II.AG为对角线,则C点坐标为(2t,yc)因为C在![]() 上,故由t的取值范围即可确定yc的取值范围.
上,故由t的取值范围即可确定yc的取值范围.
解:(1)∵P(1,3),
∴P'(﹣1,﹣3),
∴PP'2=40,
∴PC2=P'C2=40,
设C(a,b),
![]()
∴a=﹣3b,
∴b=![]() ,
,
∴C(3![]() ,﹣
,﹣![]() )或C(﹣3
)或C(﹣3![]() ,
,![]() );
);
(2))∵P(1,2),
∴P'(﹣1,﹣2),
∴PP'2=20,
∴PC2=P'C2=20,
设C(a,b),
∴![]() ,
,
∴a=﹣2b,
∴b=![]() ,
,
∴C(2![]() ,﹣
,﹣![]() )或C(﹣2
)或C(﹣2![]() ,
,![]() ),
),
∵C在第四象限,
∴C(2![]() ,﹣
,﹣![]() );
);
(3)①设P(c,![]() ),
),
∴P'(﹣c,﹣![]() ),
),
∴PP'2=![]() ,
,
PC2=P'C2=![]() ,
,
设C(s,t),
∴![]() ,
,
∴s=![]() ,
,
∴t2=3c2,
∴t=![]() ,
,
∴C![]() 或C
或C![]() ,
,
∴点C在第四象限,c>0,
∴C![]() ,
,
令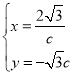 ,
,
∴xy=﹣6,即y=![]() (x>0);
(x>0);
②∵A(1,2),B(2,1),
∴经过AB直线为y=-x+3,
设G点为(t,3-t),
I. 当AG为平行四边形的边时,
∵F在y轴上,故C点横坐标为t-1,
又∵点C在y=![]() (x>0)上,
(x>0)上,
∴![]() ,
,
∵G在线段AB上,
∴1<t≤2,
∴![]() ≤-6,
≤-6,
II.当AG为对角线时,F在y轴上,故C点横坐标为2t,
∴![]() ,
,
∵G在线段AB上,
∴1<t≤2,
∴-3<![]() ≤2.
≤2.
综上所述:yc≤﹣6或﹣3<yc≤﹣2;

 中考解读考点精练系列答案
中考解读考点精练系列答案