Question

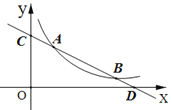
【题目】如图，点A是直线AM与⊙O的交点，点B在⊙O上，BD⊥AM，垂足为D，BD与⊙O交于点C，OC平分∠AOB，∠B＝60°．

（1）求证：AM是⊙O的切线；

（2）若⊙O的半径为4，求图中阴影部分的面积（结果保留π和根号）．

Answer 1

【答案】(1)见解析；（2）

【解析】

（1）根据题意，可得△BOC的等边三角形，进而可得∠BCO＝∠BOC，根据角平分线的性质，可证得BD∥OA，根据∠BDM＝90°，进而得到∠OAM＝90°，即可得证；

（2）连接AC，利用△AOC是等边三角形，求得∠OAC＝60°，可得∠CAD＝30°，在直角三角形中，求出CD、AD的长，则S阴影＝S梯形OADC﹣S扇形OAC即可得解．

（1）证明：∵∠B＝60°，OB＝OC，

∴△BOC是等边三角形，

∴∠1＝∠3＝60°，

∵OC平分∠AOB，

∴∠1＝∠2，

∴∠2＝∠3，

∴OA∥BD，

∵∠BDM＝90°，

∴∠OAM＝90°，

又OA为⊙O的半径，

∴AM是⊙O的切线

（2）解：连接AC，

∵∠3＝60°，OA＝OC，

∴△AOC是等边三角形，

∴∠OAC＝60°，

∴∠CAD＝30°，

∵OC＝AC＝4，

∴CD＝2，

∴AD＝2 ，

∴S阴影＝S梯形OADC﹣S扇形OAC＝ ×（4+2）×2﹣．