题目内容
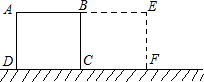 已知正方形纸片ABCD的边长AB=2cm,把正方形ABCD绕某一点按顺时针方向旋转,使它旋转后能与正方形BEFC重合.
已知正方形纸片ABCD的边长AB=2cm,把正方形ABCD绕某一点按顺时针方向旋转,使它旋转后能与正方形BEFC重合.
(1)写出满足条件的所有的旋转中心(如果原图上未标明此点,你可以在图上标明此点,并作简要说明)______.
(2)在(1)的各种情况下,分别求点A在旋转过程中所经过的路径的长.
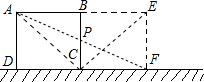 解:(1)∵正方形纸片ABCD和正方形BEFC形成了矩形,又正方形ABCD绕某一点按顺时针方向旋转,
解:(1)∵正方形纸片ABCD和正方形BEFC形成了矩形,又正方形ABCD绕某一点按顺时针方向旋转,而矩形是中心对称图形,
满足条件的所有的旋转中心有点C、点B、点P(BC的中点);
(2)以C为旋转中心:
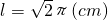 ,
,以B为旋转中心:l=3π(cm),
以P为旋转中心:
 ,
,三种单位不写总扣.
分析:(1)由于正方形纸片ABCD和正方形BEFC形成了矩形,又正方形ABCD绕某一点按顺时针方向旋转,根据矩形的性质即可确定满足条件的所有的旋转中心;
(2)分别根据旋转中心、旋转角和旋转半径即可求出点A在旋转过程中所经过的路径的长.
点评:此题分别考查了旋转的性质、正方形的性质及弧长的计算,有一定的综合性,首先利用旋转的性质和正方形的性质确定旋转中心,然后利用弧长公式计算即可求解.

练习册系列答案
相关题目
如图,在Rt△ABC纸片上可按如图所示方式剪出一正方体表面展开图,直角三角形的两直角边与正方体展开图左下角正方形的边共线,斜边恰好经过两个正方形的顶点。已知BC=24cm,则这个展开图可折成的正方体的体积为( ) 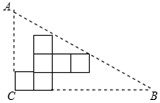
| A.64cm3 | B.27cm3 | C.9cm3 | D.8cm3 |
 (2012•路南区一模)已知:有一纸片如图,其中△ABC中,AD⊥BC,垂足为点D,BD=CD,点M在BA的延长线上.实施操作:将纸片沿一直线AN折叠,使AM和AC重合,并且过点C作CE⊥AN,垂足为点E.
(2012•路南区一模)已知:有一纸片如图,其中△ABC中,AD⊥BC,垂足为点D,BD=CD,点M在BA的延长线上.实施操作:将纸片沿一直线AN折叠,使AM和AC重合,并且过点C作CE⊥AN,垂足为点E.
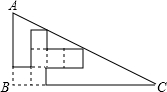 如图,在Rt△ABC纸片上可按如图所示方式剪出一正方体表面展开图,直角三角形的两直角边与正方体展开图左下角正方形的边共线,斜边恰好经过两个正方形的顶点.已知BC=24cm,则这个展开图可折成的正方体的体积为( )
如图,在Rt△ABC纸片上可按如图所示方式剪出一正方体表面展开图,直角三角形的两直角边与正方体展开图左下角正方形的边共线,斜边恰好经过两个正方形的顶点.已知BC=24cm,则这个展开图可折成的正方体的体积为( )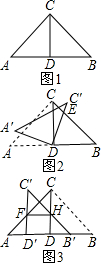 如图1,将等腰直角三角形纸片ABC沿底边上的高CD剪开,得到两个全等的三角形△ADC,△BDC,已知AC=4.
如图1,将等腰直角三角形纸片ABC沿底边上的高CD剪开,得到两个全等的三角形△ADC,△BDC,已知AC=4.