题目内容
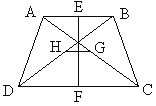
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
(1)求证:△BAE≌△BCF;
(2)若∠ABC=40°,则当∠EBA= 时,四边形BFDE是正方形.

【答案】(1)证明见解析;(2)25.
【解析】分析:(1)由菱形的性质得出AB=CB,由等腰三角形的性质得出∠BAC=∠BCA,证出∠BAE=∠BCF,由SAS证明△BAE≌△BCF即可;(2)由菱形的性质得出AC⊥BD,OA=OC,OB=OD,∠ABO=![]() ∠ABC=20°,证出OE=OF,得出四边形BFDE是菱形,证明△OBE是等腰直角三角形,得出OB=OE,BD=EF,证出四边形BFDE是矩形,即可得出结论.
∠ABC=20°,证出OE=OF,得出四边形BFDE是菱形,证明△OBE是等腰直角三角形,得出OB=OE,BD=EF,证出四边形BFDE是矩形,即可得出结论.
本题解析:
(1)证明:∵四边形ABCD是菱形,
∴AB=CB,
∴∠BAC=∠BCA,
∴180°﹣∠BAC=180°﹣∠BCA,
即∠BAE=∠BCF,
在△BAE和△BCF中, 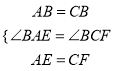 ,
,
∴△BAE≌△BCF(SAS);
(2)解:若∠ABC=40°,则当∠EBA=25°时,四边形BFDE是正方形.理由如下:
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD,∠ABO=![]() ∠ABC=20°,
∠ABC=20°,
∵AE=CF,
∴OE=OF,
∴四边形BFDE是平行四边形,
又∵AC⊥BD,∴四边形BFDE是菱形,
∵∠EBA=25°,
∴∠OBE=25°+20°=45°,
∴△OBE是等腰直角三角形,
∴OB=OE,
∴BD=EF,
∴四边形BFDE是矩形,
∴四边形BFDE是正方形;
故答案为:25.

练习册系列答案
相关题目