题目内容
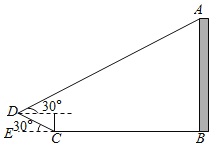
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=60°,AB=6cm,将△ABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的点D处,则AC边扫过的图形(阴影部分)的面积是_____cm2.(结果保留π).

【答案】9π
【解析】
根据直角三角形两锐角互余求出∠BAC=30°,再根据直角三角形30°角所对的直角边等于斜边的一半可得BC=![]() AB,然后求出阴影部分的面积=S扇形ABE﹣S扇形BCD,列计算即可得解.
AB,然后求出阴影部分的面积=S扇形ABE﹣S扇形BCD,列计算即可得解.
∵∠C是直角,∠ABC=60°,
∴∠BAC=90°﹣60°=30°,
∴BC=![]() AB=
AB=![]() ×6=3(cm),
×6=3(cm),
∵△ABC以点B为中心顺时针旋转得到△BDE,
∴S△BDE=S△ABC,∠ABE=∠CBD=180°﹣60°=120°,
∴阴影部分的面积=S扇形ABE+S△BDE﹣S扇形BCD﹣S△ABC
=S扇形ABE﹣S扇形BCD
=![]() ﹣
﹣![]()
=12π﹣3π
=9π(cm2).
故答案为:9π.

练习册系列答案
相关题目
【题目】国庆70周年前夕,网店销售 三种规格的手摇小国旗,其部分相关信息如下表:
型号 | 规格(mm) | 批发价(元/面) | 建议零售价(元/面) |
大号 | 45x30 | 2.00 | |
中号 | 28x20 | 1.50 | |
小号 | 22x14 |
已知大号小国旗比中号的批发价贵0.3元,小号小国旗比中号的批发价便宜0.1元某小商品零售商店,第一次用 380元购进了一批大号小国旗,紧接着又用780元购进了第二 批中号小国旗,第二批的数量是第一批的3倍.
(1)求三种型号小国旗的批发价分别是多少元?
(2)该商店很快又购进了第三批小号小国旗1200面.如果三批小国旗全部按网店建议零 售价销售完后,该零售商店获利不少于1980 元,那么小号小国旗的建议零售价至少 为多少元?