题目内容
【题目】已知抛物线y=-x2+2mx-m2+![]() 的顶点为P.
的顶点为P.
(1)求证:不论m取何值,点P始终在同一个反比例函数图象上?
(2)若抛物线与x轴交于A、B两点,当m为何值时,线段AB长等于8?
(3)该抛物线上是否存在一点Q,使得△OPQ是以点P为顶点的等腰直角三角形?若不存在,请说明理由;若存在,请求出m的值.
【答案】(1)答案见解析;(2)![]() ;(3)±1.
;(3)±1.
【解析】
(1)先求出二次函数的顶点坐标,根据反比例函数性质即可得出结论;(2)把y=0代入函数解析式得到关于m的一元二次方程,再由m>0,即可求解;(3)分m>0,m<0,两种情况讨论即可.
本题解析:
(1)证明:∵y=-x2+2mx-m2+![]() ,∴y=-(x-m)2+
,∴y=-(x-m)2+![]() ,∴P(m,
,∴P(m,![]() ).
).
∵m×![]() =1,∴点P始终在
=1,∴点P始终在![]() 图象上
图象上
(2)把y=0代入y=-x2+2mx-m2+![]() 中
中
-x2+2mx-m2+![]() =0
=0
(x-m)2=![]()
当m>0时,x=m±![]() ,∴AB=
,∴AB=![]() ,∴m=
,∴m=![]() .
.
(3)①当m>0,∠OPQ=90°时
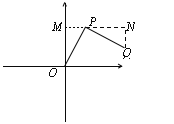
如图,可证△OPM≌△PQN.
∵P(m,![]() ),∴Q(m+
),∴Q(m+![]() ,
,![]() -m)(注:抛物线开口向下,只有这一种情况)
-m)(注:抛物线开口向下,只有这一种情况)
∴![]() -m=-(m+
-m=-(m+![]() -m)2+
-m)2+![]() ,解得m=1.
,解得m=1.
②当m<0,∠OPQ=90°时
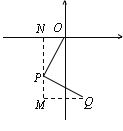
∵P(m,![]() ),∴Q(m-
),∴Q(m-![]() ,
,![]() +m) (注:抛物线开口向下,只有这一种情况)
+m) (注:抛物线开口向下,只有这一种情况)
∴![]() +m=-(m-
+m=-(m-![]() -m)2+
-m)2+![]() ,解得m=-1.
,解得m=-1.
综上所述:m的值为±1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目