题目内容
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于A,B两点,其中点A(-1,0),点C(0,5),点D(1,8)都在抛物线上,已知M为抛物线的顶点.

(1)求抛物线的表达式;
(2)求△MCB的面积;
(3)根据图形直接写出使直线MC表示的一次函数值大于二次函数值的x的取值范围.
【答案】(1)y=-x2+4x+5;(2)15;(3)x<0或x>2.
【解析】试题分析:利用待定系数法,列方程组求二次函数解析式.
(2)先求出M点坐标,利用S△BCM=S△OCM+S△BOM-S△OBC 分别求出S△OCM,S△BOM,S△OBC
作差就可以算出△MCB的面积.
(3)直线MC图象比二次函数图象高的部分.
试题解析:
(1)∵A(-1,0),C(0,5),D(1,8)三点在抛物线y=ax2+bx+c上,
∴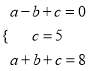 ,解得
,解得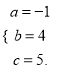
∴抛物线的表达式为y=-x2+4x+5.
(2)连接OM,BM.
∵y=-x2+4x+5=-(x-2)2+9,
∴M(2,9).
∵抛物线的对称轴为直线x=2,A(-1,0),
∴B(5,0).
∴S△BCM=S△OCM+S△BOM-S△OBC
=![]() ×5×2+
×5×2+![]() ×5×9-
×5×9-![]() ×5×5
×5×5
=15.
(3)x<0或x>2.

练习册系列答案
相关题目
【题目】(7分)某产品每件的成本10元,试销阶段每件产品的销售价![]() (元)与产品的日销售量
(元)与产品的日销售量![]() (件)之间的关系如下表:
(件)之间的关系如下表:
| 15 | 20 | 30 | … |
| 25 | 20 | 10 | … |
且日销售量![]() (件)是销售价
(件)是销售价![]() (元)的一次函数.
(元)的一次函数.
(1)求出日销售量![]() (件)与销售价
(件)与销售价![]() (元)的函数关系式;
(元)的函数关系式;
(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时最大销售利润是多少?



